Graphs
The subject of graph theory was initiated by Leonhard Euler. He used it to solve the famous Königsberg bridge problem, which we will discuss later in this chapter.
Graph theory has turned out to be an important tool for solving problems in many fields. For example, one can model the internet by representing webpages as dots and hyperlinks as arrows from one dot to another. Google’s PageRank algorithm was developed by Larry Page and Sergey Brin using ideas from graph theory. Social networks and power infrastructures can also be represented as graphs. By analysing the graph one can determine which nodes have the most influence, or one can evaluate the vulnerability of a network against failure or attack. Facebook and other social network companies use information obtained from the graph as a marketing tool and for offering improved services. For example, graph theory can tell whether a circuit can be implemented on a planar circuit board. It is possible to distinguish between two chemical compounds with the same molecular formula but different structures using graphs. Computer and communication networks are often modelled using graphs. We can determine whether two computers are connected by a communications link using graph models of computer networks. Problems such as finding the shortest tour through a number of cities can be expressed and solved using graph theory, and are a key component of GPS-based navigation systems. There are many more applications.
Introduction to graphs
Graphs are discrete structures formed of dots (called vertices) and lines (called edges or arcs) that run between the vertices.
Examples of graphs
Link copiedNote that all the roads are two-way roads (can drive from Auckland to Hamilton or from Hamilton to Auckland along the same road).

Note that there is at most one cable between two computers in this network and that each cable operates in both directions. In other words, this network can be modeled using a simple graph.
Definition 5.1 A simple graph consists of , a nonempty set of vertices, and , a set of unordered pairs of distinct elements of called edges.
Multigraphs
Link copiedSometimes there are multiple optical cables between computers in a network. This is the case when there is heavy traffic between computers. A network with multiple lines is displayed below. Simple graphs may not be sufficient to model such networks. Instead, multigraphs are used, which consist of vertices and undirected edges between these vertices, with multiple edges between pairs of vertices allowed.
Every simple graph is also a multigraph. However, not all multigraphs are simple graphs, since in a multigraph two or more edges may connect the same pair of vertices.

We cannot use a pair of vertices to specify an edge of a graph when multiple edges are present. This makes the formal definition of multigraphs somewhat complicated.
Definition 5.2 A Multigraph consists of a set of vertices, a set of edges, and a function from to . The edges and are called multiple or parallel edges if .
Loops and pseudographs
Link copied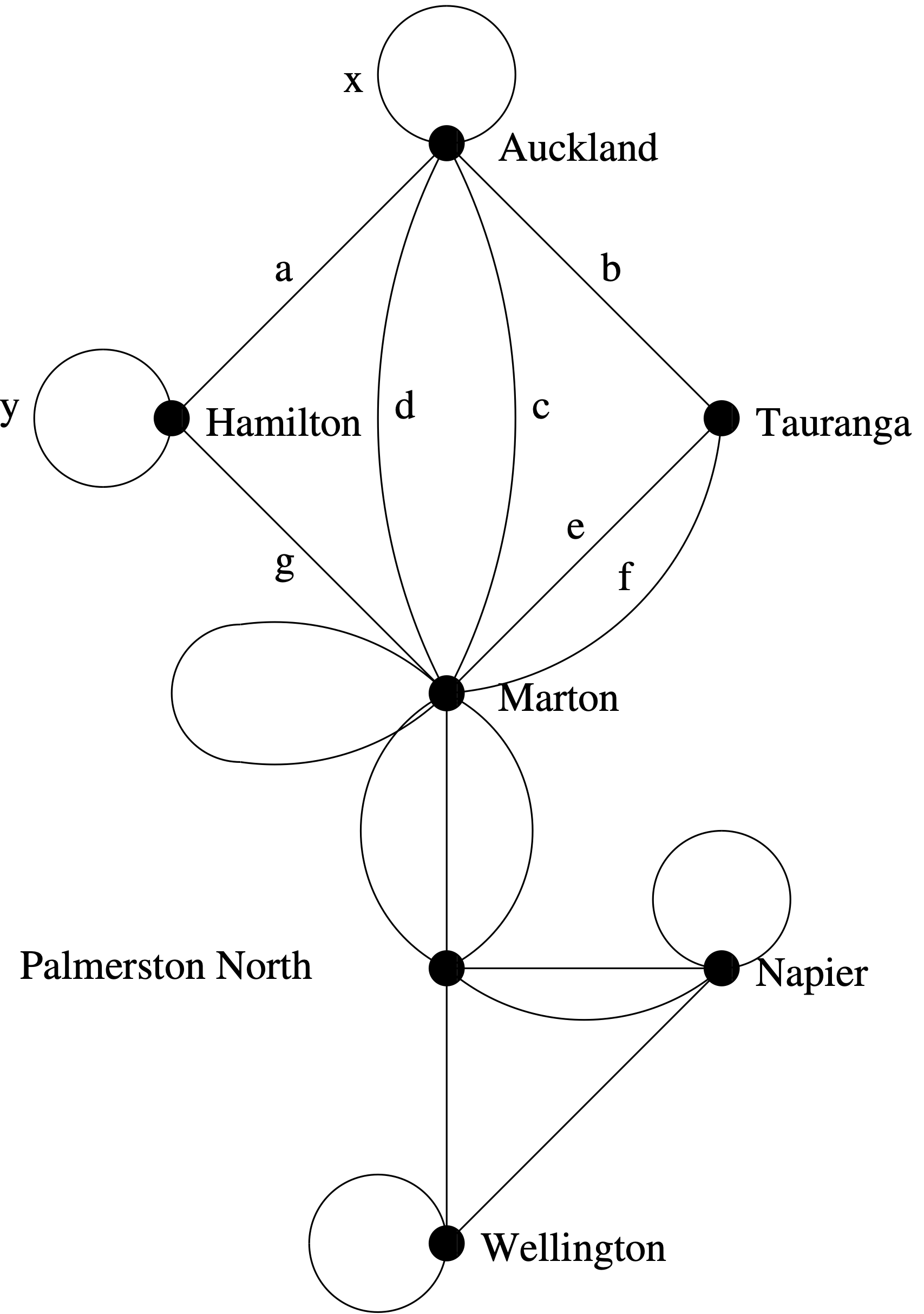
Definition 5.3 A pseudograph _consists of a set of vertices, a set of edges, and a function from to . An edge is a loop if for some .
We often say ” is an edge of ” for a graph if there is at least one edge with .
To summarize, pseudographs are the most general type of undirected graphs since they may contain loops and multiple edges. Multigraphs are undirected graphs that may contain multiple edges but may not have loops. Finally, simple graphs are undirected graphs with no multiple edges or loops.
Directed graphs
Link copied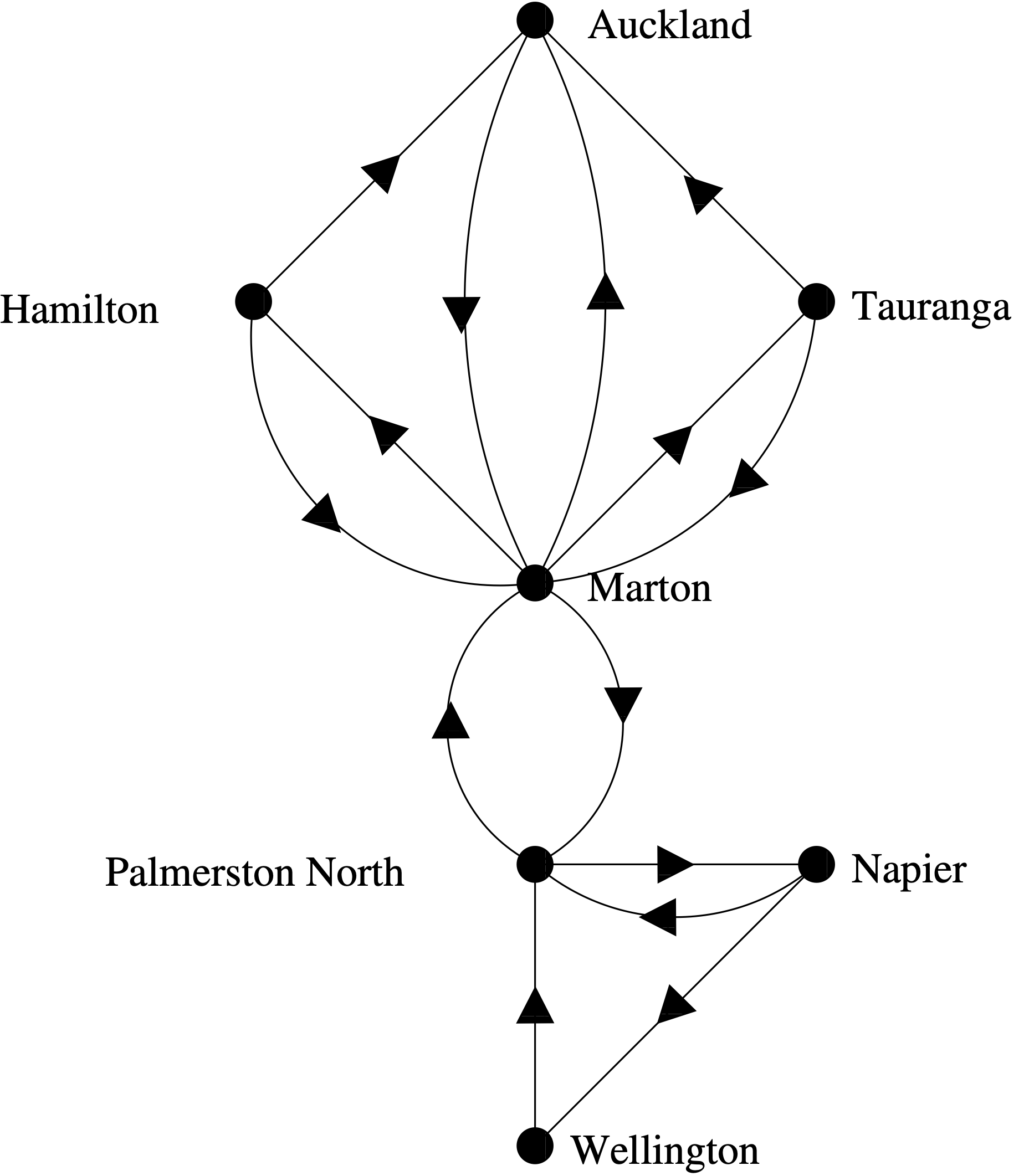
We use directed graphs to model such networks. The edges of a directed graph are ordered pairs rather than sets. Loops, ordered pairs of the same element, and multiple edges in the same direction between two vertices are not allowed.
Definition 5.4 A directed graph consists of a set of vertices and a set of edges that are ordered pairs of elements of .
Directed multigraphs
Link copied
Directed graphs are not sufficient for modeling such a network, since multiple edges are not allowed in these graphs. Instead we use directed multigraphs. Loops are not allowed in directed multigraphs.
Definition 5.5 A directed multigraph consists of a set of vertices, a set of edges, _and a function from to . The edges and are multiple edges if
As before, we will say that is an edge of as long as there is at least one edge with . We will often interchangeably use the edge and the ordered pair associated to it, unless the identity of individual multiple edges is important.
Directed pseudograph
Link copied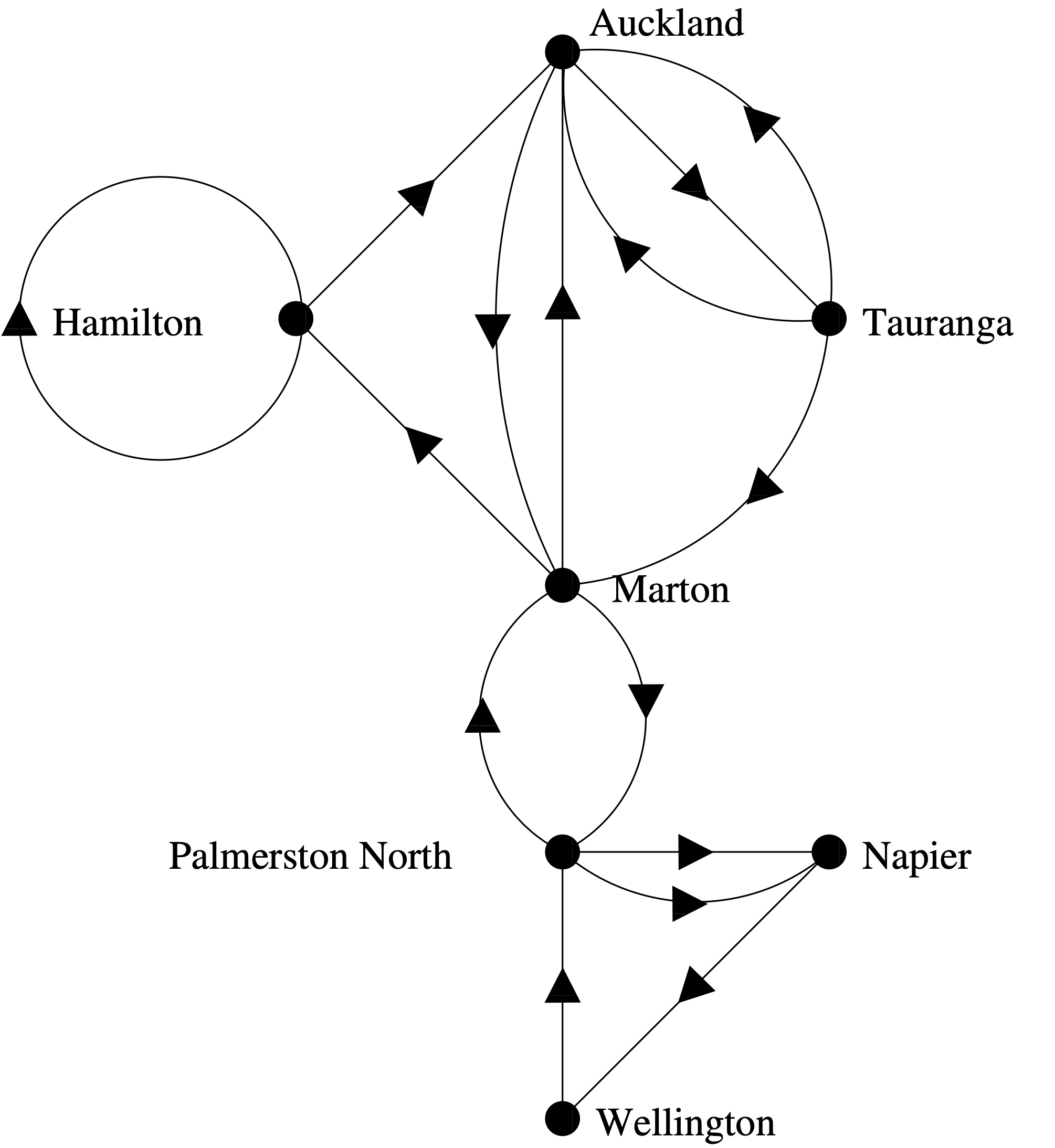
Directed multigraphs are not sufficient for modeling such a network, since loops are not allowed in these graphs. Instead we use directed pseudograph.
Definition 5.6 A directed pseudograph consists of a set of vertices, a set of edges, and a function from to The edges and are multiple edges if
As before, we will say that is an edge of as long as there is at least one edge with . We will often interchangeably use the edge and the ordered pair associated to it, unless the identity of individual multiple edges is important.
Then the graph is pictured below.
Summary of terminology
Link copiedThe definitions of the various types of graphs are summarized in the table below.
Graph theory has been applied and developed in a wide range of subjects and applications. Hence, the terminology is not completely standard. When reading other books and webpages you should be careful that the notions “graph” and “multigraph” may have slightly different meanings.
| Type | Edges | Multiple Edges Allowed? | Loops Allowed? |
|---|---|---|---|
| Simple graph | Undirected | No | No |
| Multigraph | Undirected | Yes | No |
| Pseudograph | Undirected | Yes | Yes |
| Directed graph | Directed | No | No |
| Directed multigraph | Directed | Yes | No | Directed pseudograph | Directed | Yes | Yes |
Basic terminology
We introduce some basic vocabulary used in graph theory.
Terminology on vertices and edges
Link copiedDefinition 5.7 Two vertices and in an undirected graph are called adjacent (or neighbors) in if is an edge of . If , the edge is called incident with the vertices and . The edge is also said to connect and . The vertices and are called endpoints _of the edge .
Degree
Link copiedTo keep track of how many edges are incident to a vertex, we make the following definition.
Definition 5.8 The degree of a vertex in an undirected graph is the number of edges incident with it, except that a loop at a vertex contributes twice to the degree of that vertex. The degree of the vertex is denoted by .
The handshaking theorem
Link copiedEvery edge is incident with exactly two (possibly equal) vertices. Hence, the sum of the degrees of the vertices is twice the number of edges. This result is sometimes called the Handshaking Theorem, because of the analogy between an edge having two endpoints and a handshake involving two hands.
Theorem 5.1 [The Handshaking Theorem] Let be an undirected graph with edges. Then
(Note this applies even if multiple edges and loops are present.)
Proof: See lecture.
Theorem 5.1 shows that the sum of the degrees of the vertices of an undirected graph is even. This simple fact has many consequences, one of which is given as Theorem 5.2.
Theorem 5.2 An undirected graph has an even number of vertices of odd degree.
Proof: See lecture.
Definition 5.9 The degree sequence of a graph is the sequence , where is the number of vertices of degree , , and does not have any vertices of degree greater than .


Terminology for directed graphs
Link copiedWe now give some useful terminology for graphs with directed edges.
Definition 5.10 When is an edge of the graph with directed edges, is said to be adjacent to and is said to be adjacent from . The vertex is called the initial vertex of , and is called the terminal or end vertex of . The initial vertex and terminal vertex of a loop are the same. We say an edge is outgoing from and ingoing to .
In-degree and out-degree
Link copiedDefinition 5.11 In a graph with directed edges the in-degree of a vertex , denoted by , is the number of edges with as their terminal vertex. The out-degree of , denoted by , is the number of edges with as their initial vertex. (Note that a loop at a vertex contributes 1 to both the in-degree and the out-degree of this vertex.)
Since each edge has an initial vertex and a terminal vertex, the sum of the in-degrees and the sum of the out-degrees of all vertices in a graph with directed edges are the same. Both of these sums are the number of edges in the graph. This result is stated as the following theorem.
Theorem 5.3 _Let be a graph with directed edges. Then
Underlying graph
Link copiedThere are many properties of a graph with directed edges that do not depend on the direction of its edges. Consequently, it is often useful to ignore these directions. The undirected graph that results from ignoring directions of edges is called the underlying undirected graph. A graph with directed edges and its underlying undirected graph have the same number of edges.
We will now introduce several classes of simple graphs. These graphs are often used as examples and arise in many applications.
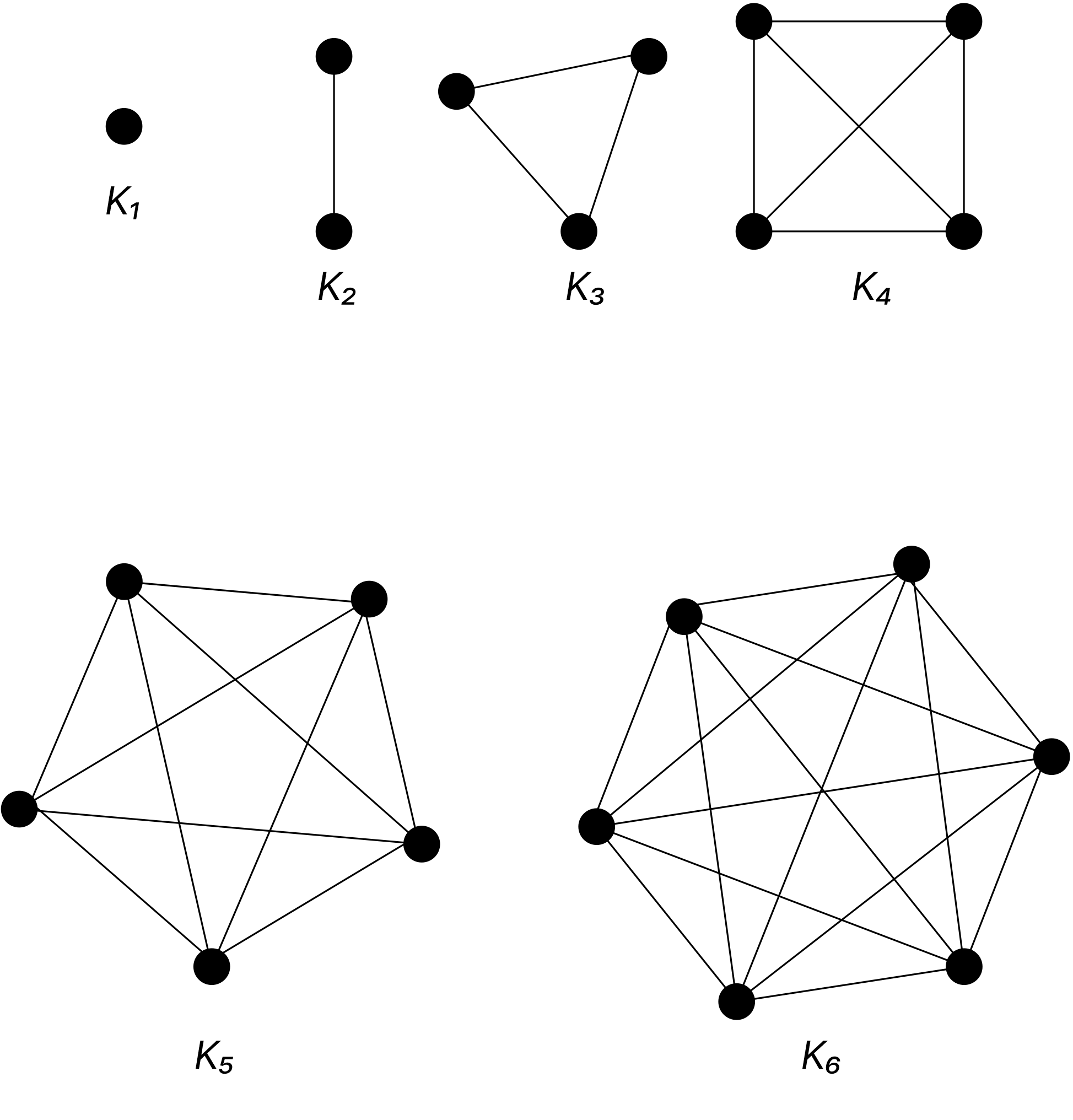
Complete graphs
Link copiedThe complete graph on vertices, denoted by , is the simple graph that contains exactly one edge between each pair of distinct vertices. The graphs , for are displayed below.
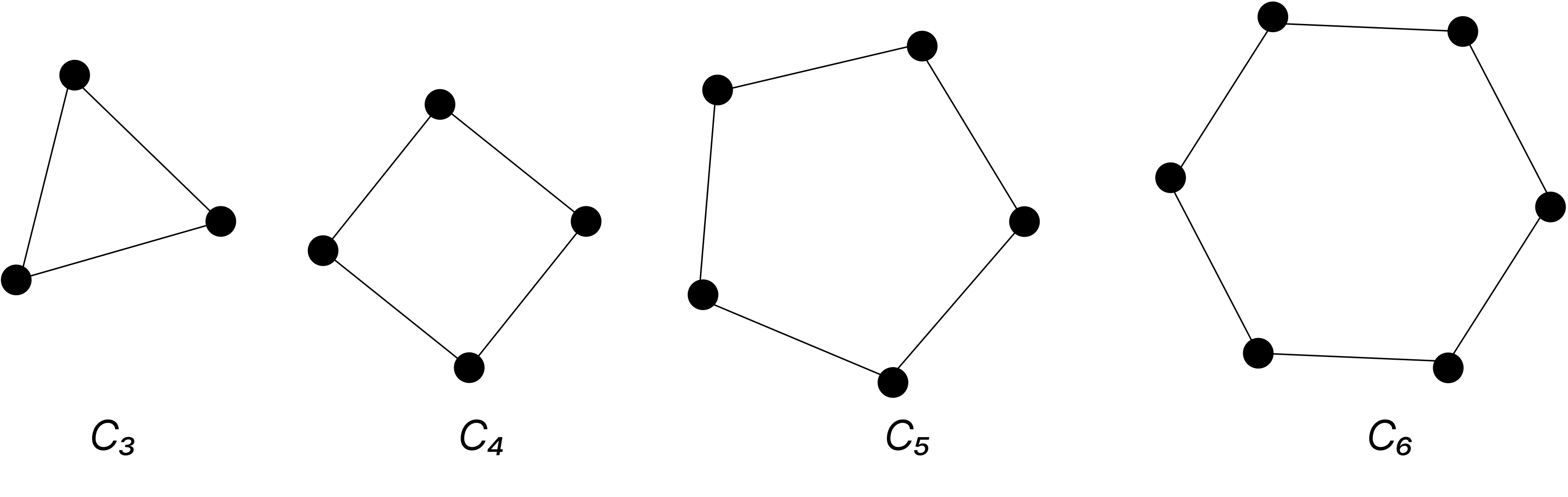
Cycle graphs
Link copiedThe cycle_ graph , consists of n vertices and edges and The cycle graphs , and are displayed below.
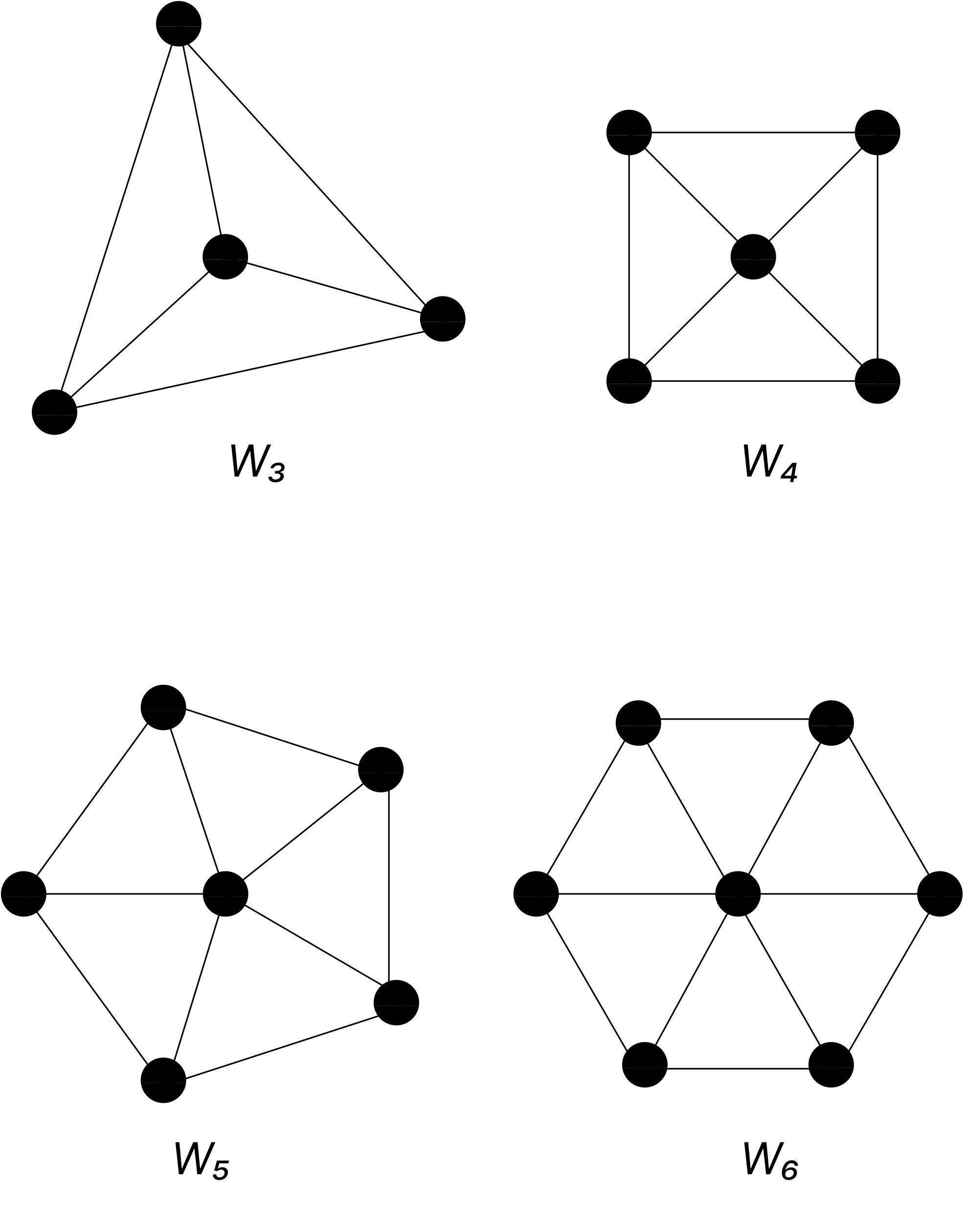
Wheel graphs
Link copiedWe obtain the wheel graph when we add an additional vertex to the cycle , for , and connect this new vertex to each of the vertices in by new edges. The wheel graphs , and are displayed below.
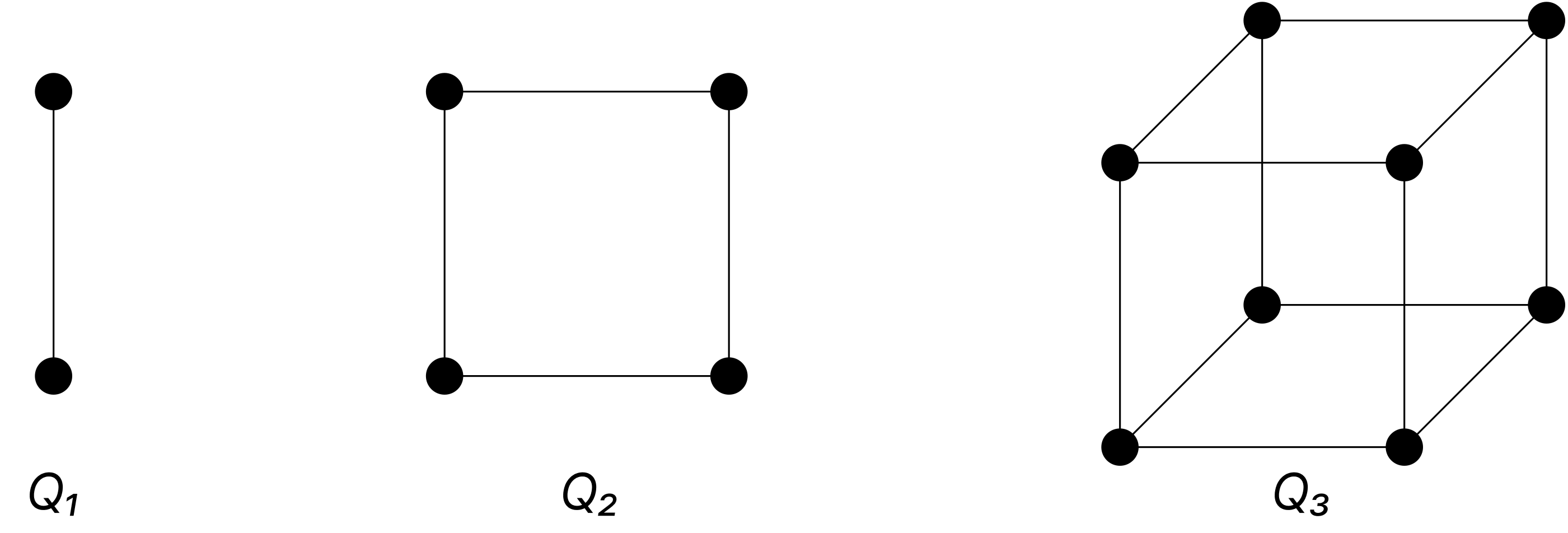
-Cubes
The -cube, denoted by is the graph that has vertices representing the bit strings of length . Two vertices are adjacent if and only if the bit strings that they represent differ in exactly one bit position. The graphs , and are displayed below.
Bipartite graphs
Link copiedSometimes a graph has the property that its vertex set can be divided into two disjoint subsets such that each edge connects a vertex in one of these subsets to a vertex in the other subset. For example, consider the graph representing all the students in this class and the set of courses they are taking. We draw an edge between a student and a course if the student is taking that course. The vertex set is the union where is the set of students and is the set of courses.
Definition 5.12 A simple graph is called bipartite if its vertex set can be partitioned into two disjoint nonempty sets and such that every edge in the graph connects a vertex in and a vertex in (so that no edge in connects either two vertices in or two vertices in ).
Complete bipartite graphs
Link copiedThe complete bipartite graph is the graph that has its vertex set partitioned into two subsets of and vertices, respectively. There is an edge between two vertices if and only if one vertex is in the first subset and the other vertex is in the second subset.
Subgraphs
Link copiedSometimes we need only part of a graph to solve a problem. For instance, we may care only about one part of a large computer network, such as the part that involves the data centres in Auckland, Hamilton, Wellington, and Christchurch. We can ignore the other centres and cables. In the graph model we remove the vertices corresponding to the computer centres other than the four of interest, and we remove all edges incident with any vertex that was removed.
When edges and vertices are removed from a graph, without removing endpoints of any remaining edges, a smaller graph is obtained. Such a graph is called a subgrap of the original graph.
Definition 5.13 A subgraph of a graph is a graph where and .
Notice that, in the definition of a subgraph, we must remove any edges which have had one of their endpoints removed. This does not mean that we may not also remove some of the other edges. For example, for any graph , the graph counts as a (rather uninteresting) example of a subgraph.
For example, the graph below has as a subgraph, because we can delete the “inside” vertices and edges to have just a left over.
Note that any graph is “trivially” a subgraph of itself, as we can just delete “nothing” from and have left over.

Union of two graphs
Link copiedTwo or more graphs can be combined in various ways. The new graph that contains all the vertices and edges of these graphs is called the union of the graphs. We will give a more formal definition for the union of two simple graphs.
Definition 5.14 The union _of two simple graphs and is the simple graph with vertex set and edge set The union of and is denoted by . (Note: we assume .)

Representing graphs
There are many useful ways to represent graphs. When working with graphs, it is helpful to be able to choose the most convenient representation. In this section we will show how to represent graphs in several different ways.
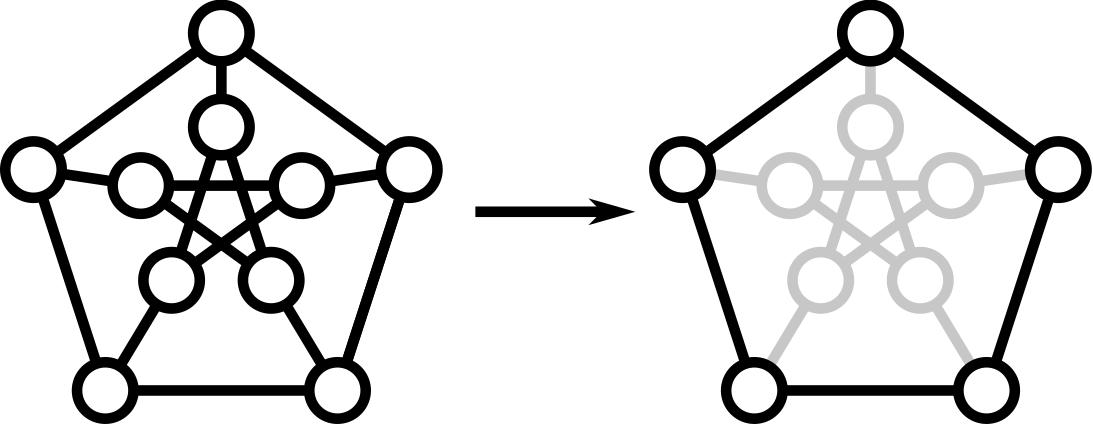
Sometimes, two graphs have exactly the same structure, in the sense that there is a one-to-one correspondence between their vertex sets that preserves edges. In such a case, we say that the two graphs are isomorphic. Determining whether two graphs are isomorphic is an important problem of graph theory.
Adjacency lists
Link copiedOne way to represent a graph without multiple edges is to list all the edges of this graph. Another way to represent a graph with no multiple edges is to use adjacency lists, which specify the vertices that are adjacent to each vertex of the graph.
Adjacency matrices
Link copiedCarrying out graph algorithms using the representation of graphs by lists of edges, or by adjacency lists, can be cumbersome if there are many edges in the graph. To simplify computation, graphs can be represented using matrices. Two types of matrices commonly used to represent graphs will be presented here. One is based on the adjacency of vertices, and the other is based on incidence of vertices and edges.
Suppose that is a simple graph where . Suppose that the vertices of are listed as . The adjacency matrix (or ) of G with respect to this listing of the vertices, is the zero-one matrix with 1 as its th entry when and are adjacent, and 0 as its th entry when they are not adjacent. In other words, if its adjacency matrix is , then
a_{ij}=\left\{\begin{array}{ll} 1 & if \{v_{i},v_{j}, \} \text {is an edge of} G\\ 0 & otherwise\\ \end{array}\right}Note that an adjacency matrix of a graph is based on the ordering chosen for the vertices. Hence, there are potentially as many as different adjacency matrices for a graph with vertices, since there are different orderings of vertices. However, once a listing of the vertices has been decided, the adjacency matrix is uniquely determined by the graph.
The adjacency matrix of a simple graph is symmetric, meaning that , since both of these entries are 1 when and are adjacent, and both are 0 otherwise. Furthermore, since a simple graph has no loops, each entry , , s 0.
Adjacency matrices can also be used to represent undirected graphs with loops and with multiple edges. A loop at the vertex is represented by a 1 at the th position of the adjacency matrix. When multiple edges are present, the adjacency matrix is no longer a zero-one matrix, since the th entry of this matrix equals the number of edges that are associated to . All undirected graphs, including multigraphs and pseudographs, have symmetric adjacency matrices.
The adjacency matrix for a directed graph does not have to be symmetric, since there may not be an edge from to when there is an edge from to . Adjacency matrices can also be used to represent directed multigraphs. Again, such matrices are not zero-one matrices when there are multiple edges in the same direction connecting two vertices In the adjacency matrix for a directed multigraph, equals the number of edges that are associated to .
Connectivity, paths and circuits
Many problems can be studied by considering paths formed by traveling along the edges of graphs. For instance, the problem of determining whether a message can be sent between two computers using intermediate links can be studied with a graph model.
Paths and circuits
Link copiedWe begin by defining the basic terminology of paths and circuits.
Definition 5.15
-
A walk of length from to , where is a non-negative integer, in an undirected graph is a sequence of edges of the graph such that , , where and . When the graph is simple, we denote this path by its vertex sequence (since listing these vertices uniquely determines the path).
-
The walk is a circuit if it begins and ends at the same vertex, that is, if . The walk or circuit is said to pass through or traverse _the vertices .
-
The circuit is a cycle if each vertex, except for the first and the last ones, only appears once._
-
The walk is a path if it does not contain the same vertex more than once._
When it is not necessary to distinguish between multiple edges, we will denote a path where for by its vertex sequence . This notation identifies a path only up to the vertices it passes through. There may be more than one path that passes through this sequence of vertices.
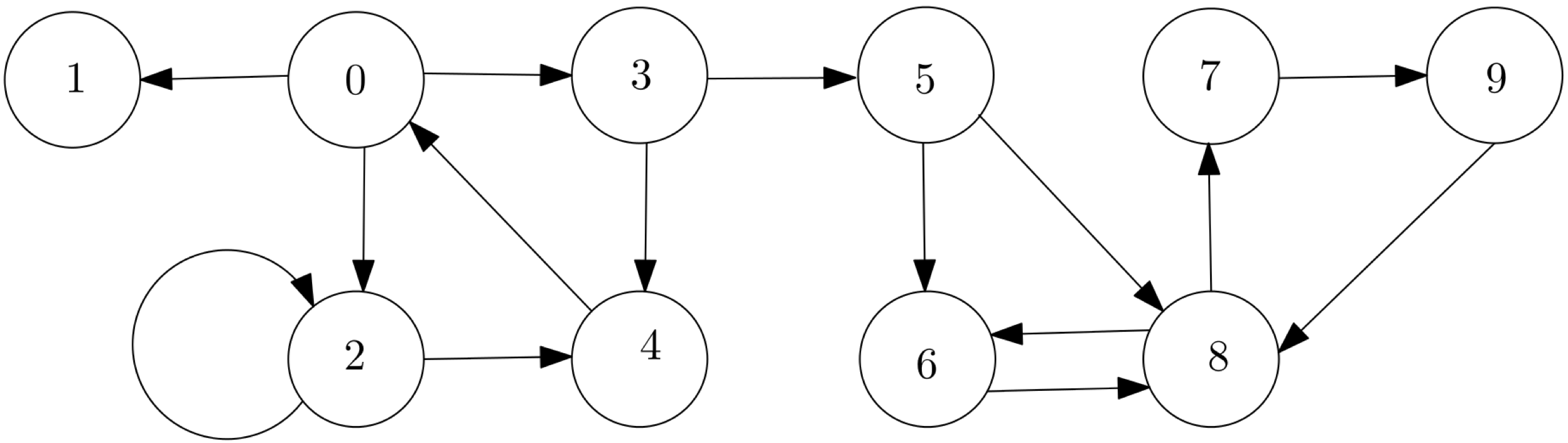
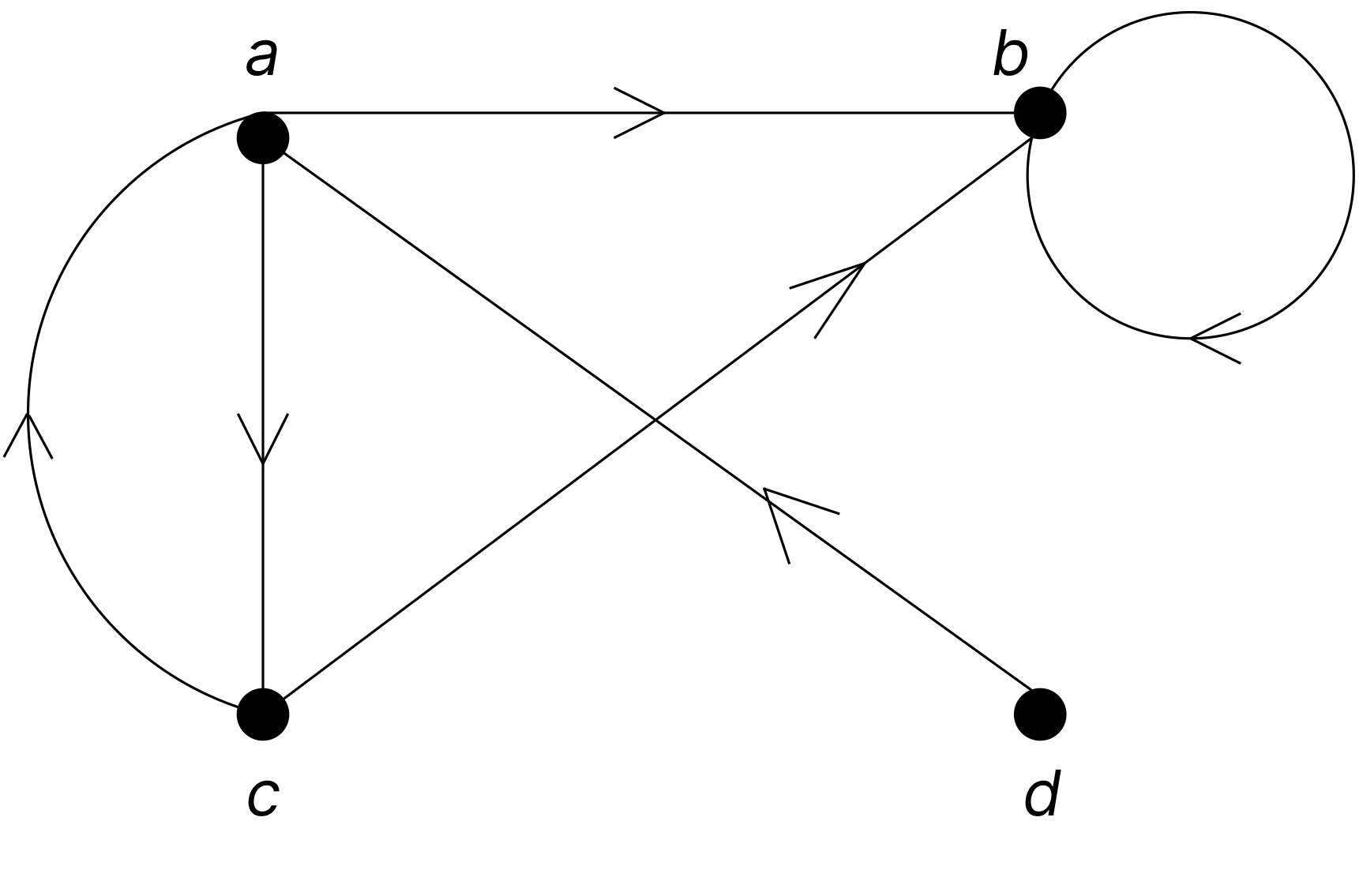
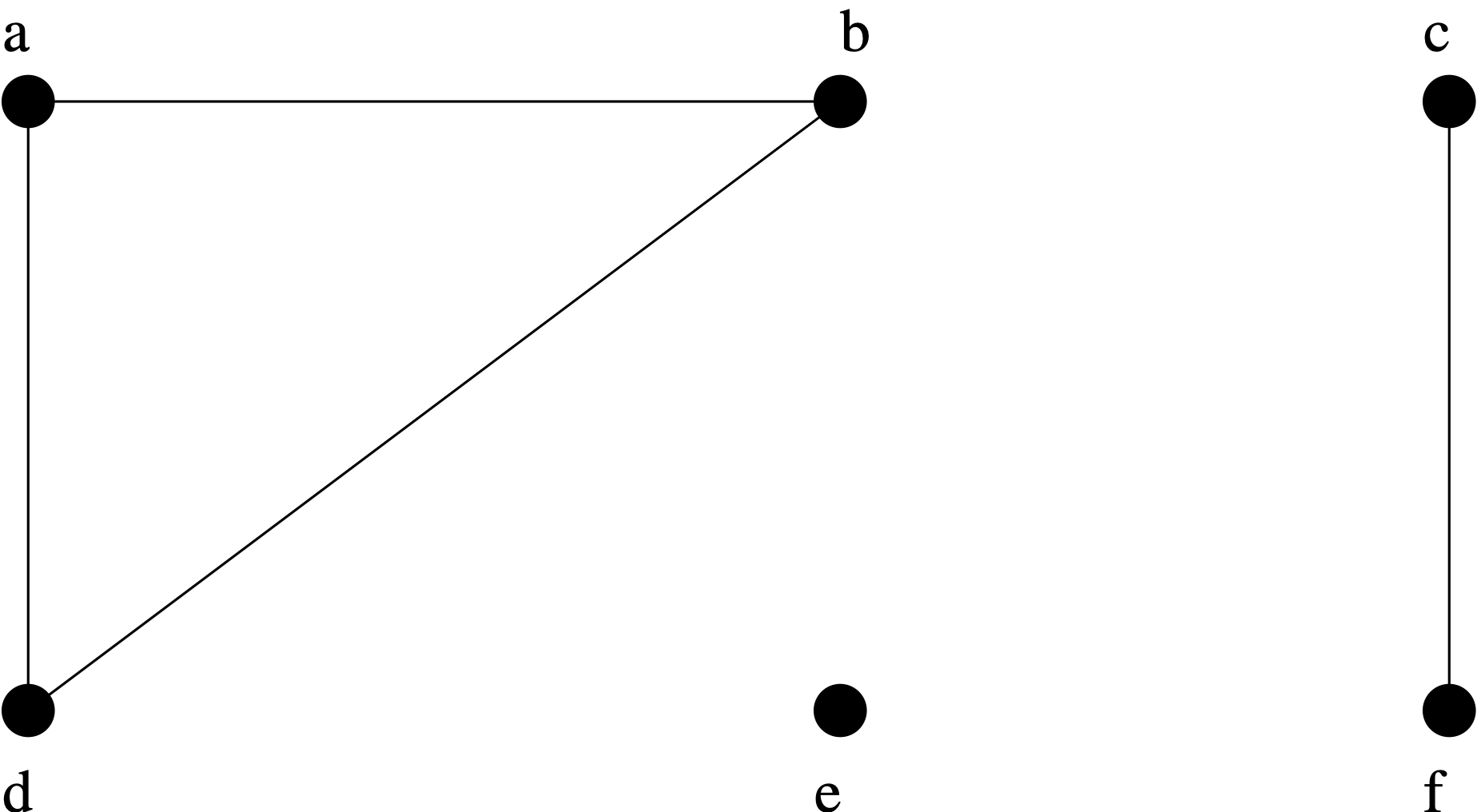
Example 5.24 _In the simple graph given below, show that is a path of length 4. Why is is not a walk? Show that is a circuit but not a cycle. What is the length of the circuit ? Why is not a path?
Theorem 5.4 Let be a graph and let . If there is a walk from to then there is a path from to .
Proof: See lecture.
Theorem 5.5 Let be a graph and let . If there is a walk from to and a walk from to then there is a walk from to .
Proof: See lecture.
Connectedness in undirected graphs
Link copiedA fundamental problem is to determine whether or not a network has the property that every pair of nodes can communicate with one another. For example, in a network of computers or data centres, two devices can communicate if there is a a cable between them or if their messages can be sent through one or more intermediate computers. If the network is represented by a graph, where edges represent the communication links, this problem becomes: When is there always a walk between two vertices in the graph?
Definition 5.16 An undirected graph is called connected if there is a walk between every pair of distinct vertices of the graph.
For this definition we always allow a walk of length from a vertex to itself.
Thus, any two computers in the network can communicate if and only if the graph of this network is connected.
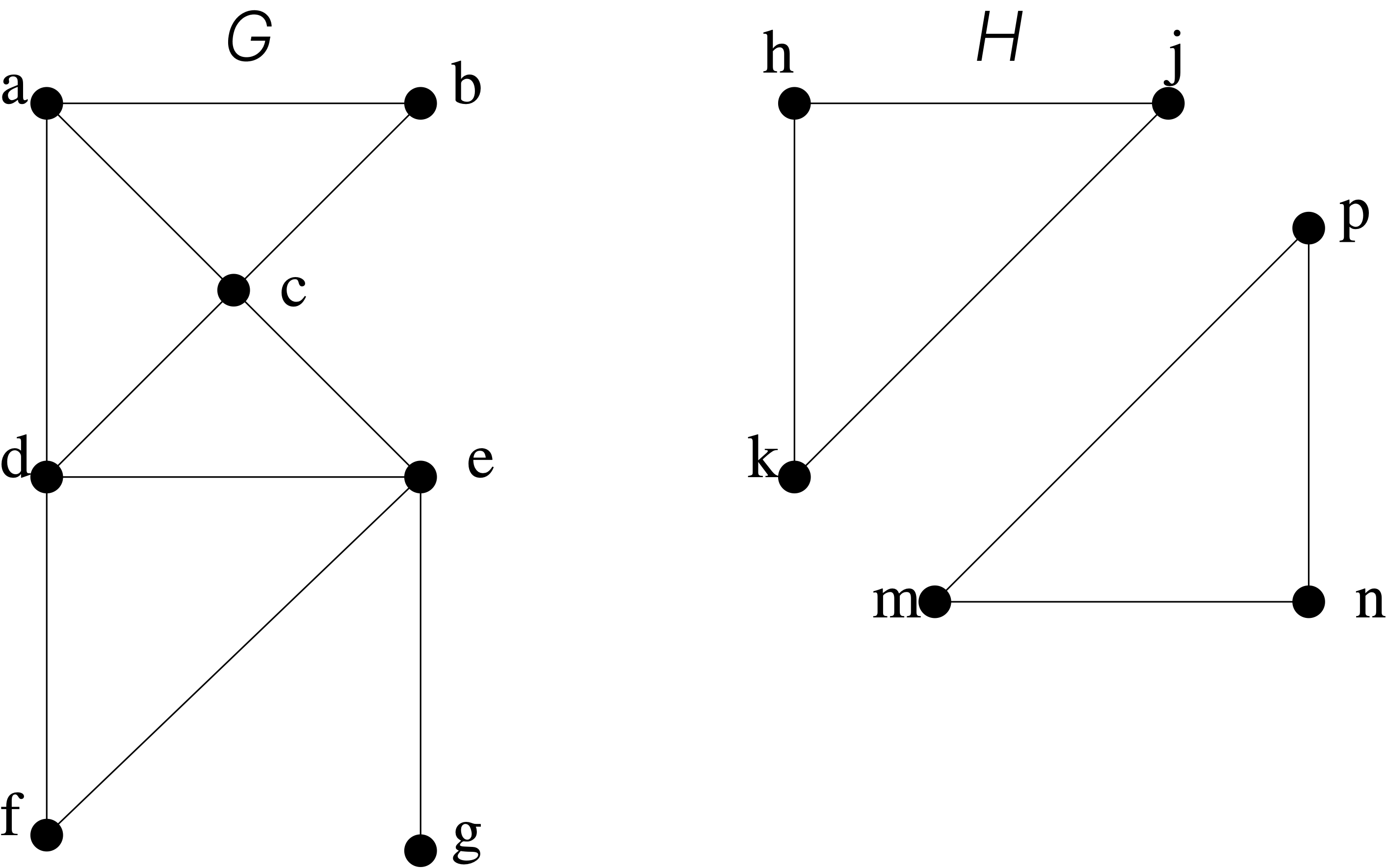
Theorem 5.6 There is a path between every pair of distinct vertices of a connected undirected graph.
Proof: See lecture.
Components
Link copiedA graph that is not connected is the union of two or more connected graphs, each pair of which has no vertex in common. These disjoint connected graphs are called the connected components of the graph.
Paths and circuits in directed multigraphs
Link copiedDefinition 5.17
-
A walk of length , where is a positive integer, from to in a directed multigraph is a sequence of edges of the graph such that where and . When there are no multiple edges in the graph, this path is denoted by its vertex sequence .
-
A walk that begins and ends at the same vertex is called a circuit.
-
A circuit is called a cycle if each vertex, except for the first and the last ones, only appears once.
-
A walk is called a path it does not contain the same vertex more than once.
When it is not necessary to distinguish between multiple edges, we will denote a path where for by its vertex sequence . The notation identifies a path only up to the vertices it passes through. There may be more than one path that passes through this sequence of vertices.
Connectedness in directed graphs
Link copiedThere are two notions of connectedness in directed graphs, depending on whether the directions of the edges are considered. Again we declare that a vertex is always strongly connected with itself (by a walk of length zero).
Definition 5.18 Two vertices in a directed graph are strongly connected if there is a walk from to and a walk from to .
A directed graph is strongly connected if there is a walk from to and a walk from to whenever and are vertices in the graph.
For a directed graph to be strongly connected there must be a sequence of directed edges from any vertex in the graph to any other vertex. A directed graph can fail to be strongly connected but still be in “one piece.” To make this precise, the following definition is given.
Definition 5.19 A directed graph is weakly connected if there is a walk between any two vertices in the underlying undirected graph.
That is, a directed graph is weakly connected if and only if there is always a walk between two vertices when the directions of the edges are disregarded. Clearly, any strongly connected directed graph is also weakly connected.
Theorem 5.7 Let be a directed graph.
- Every vertex is strongly connected to itself._
- Let . If is strongly connected to then is strongly connected to .
- Let . If is strongly connected to and is strongly connected to then is strongly connected to .
Proof: See lecture.
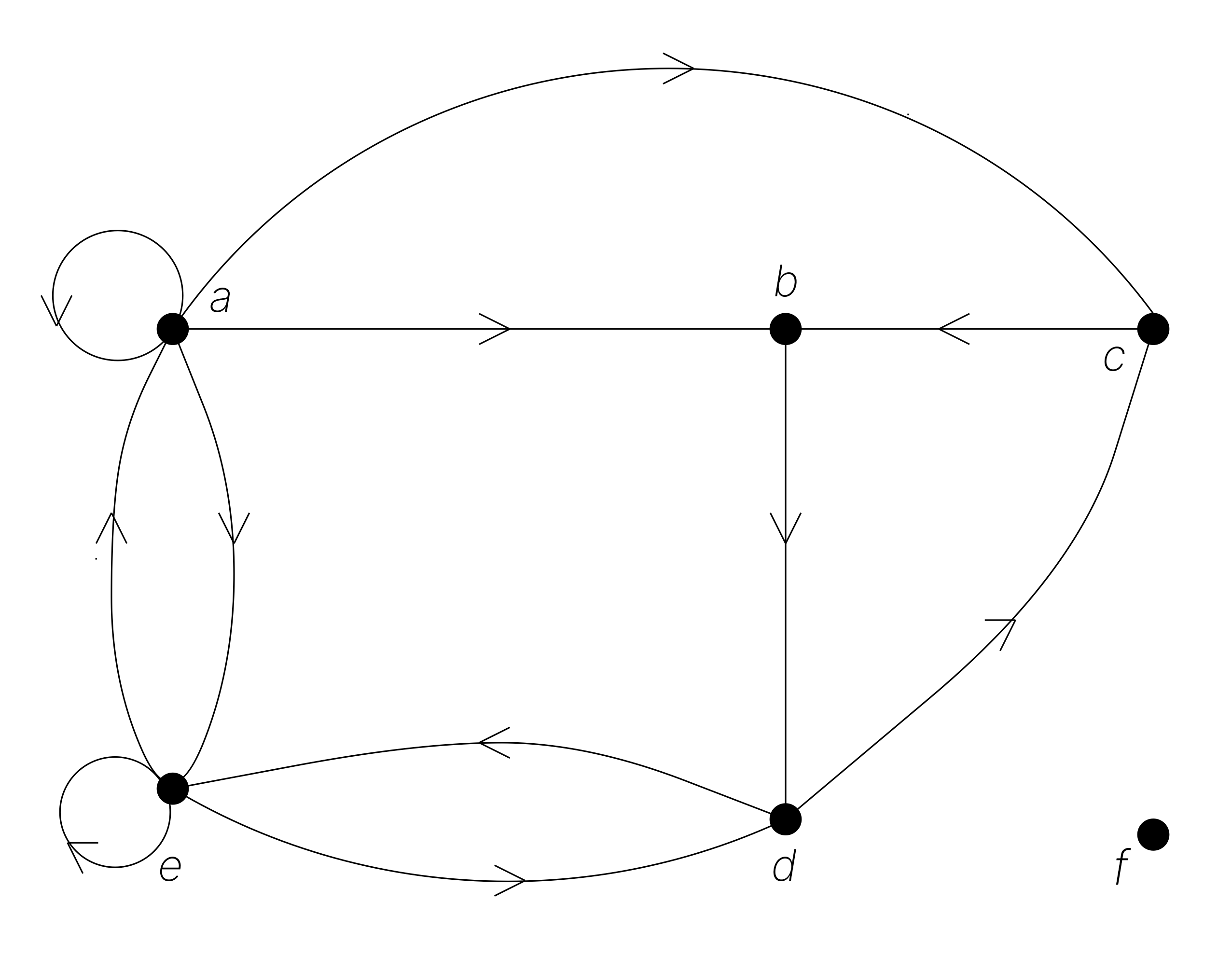
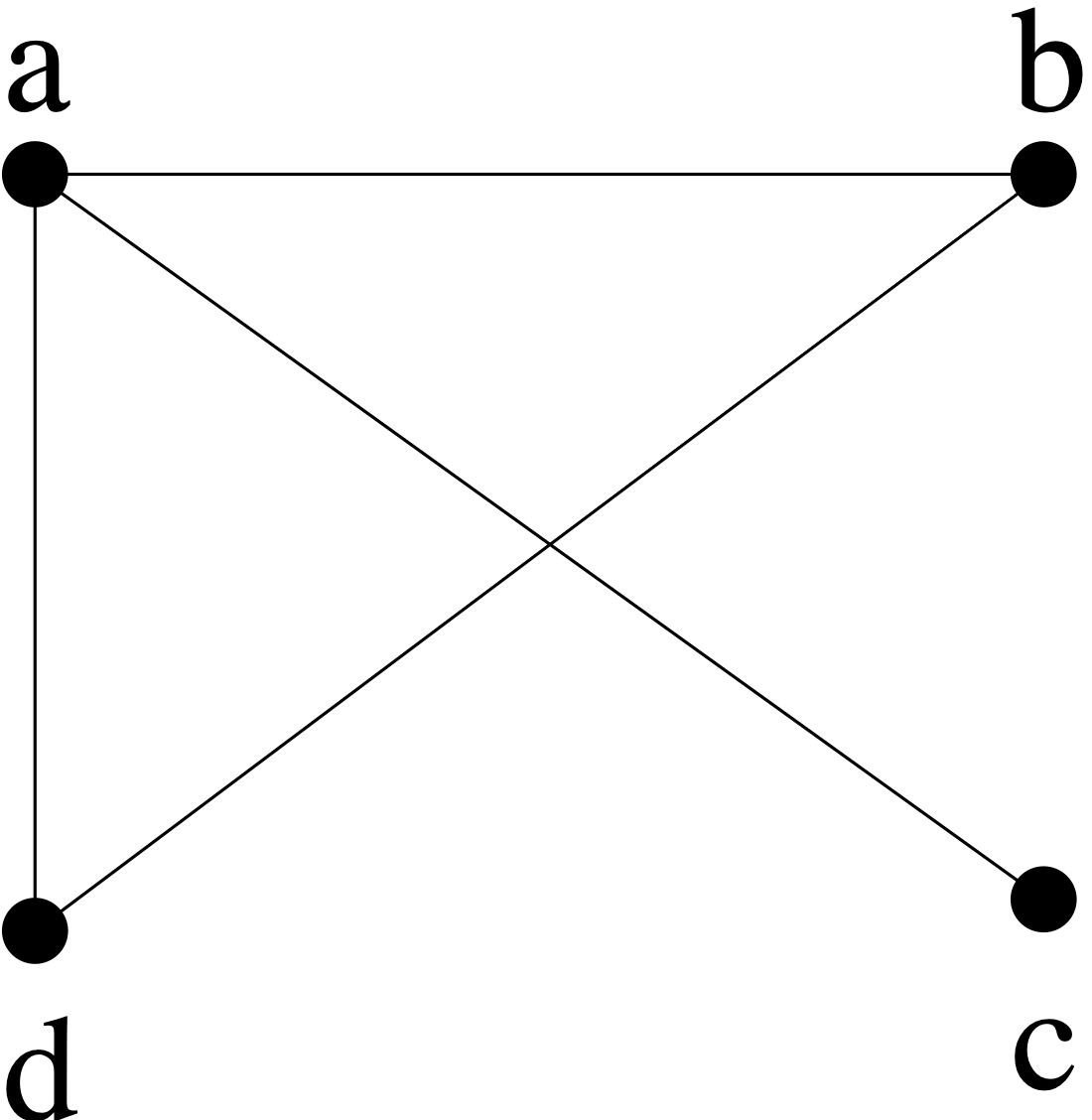
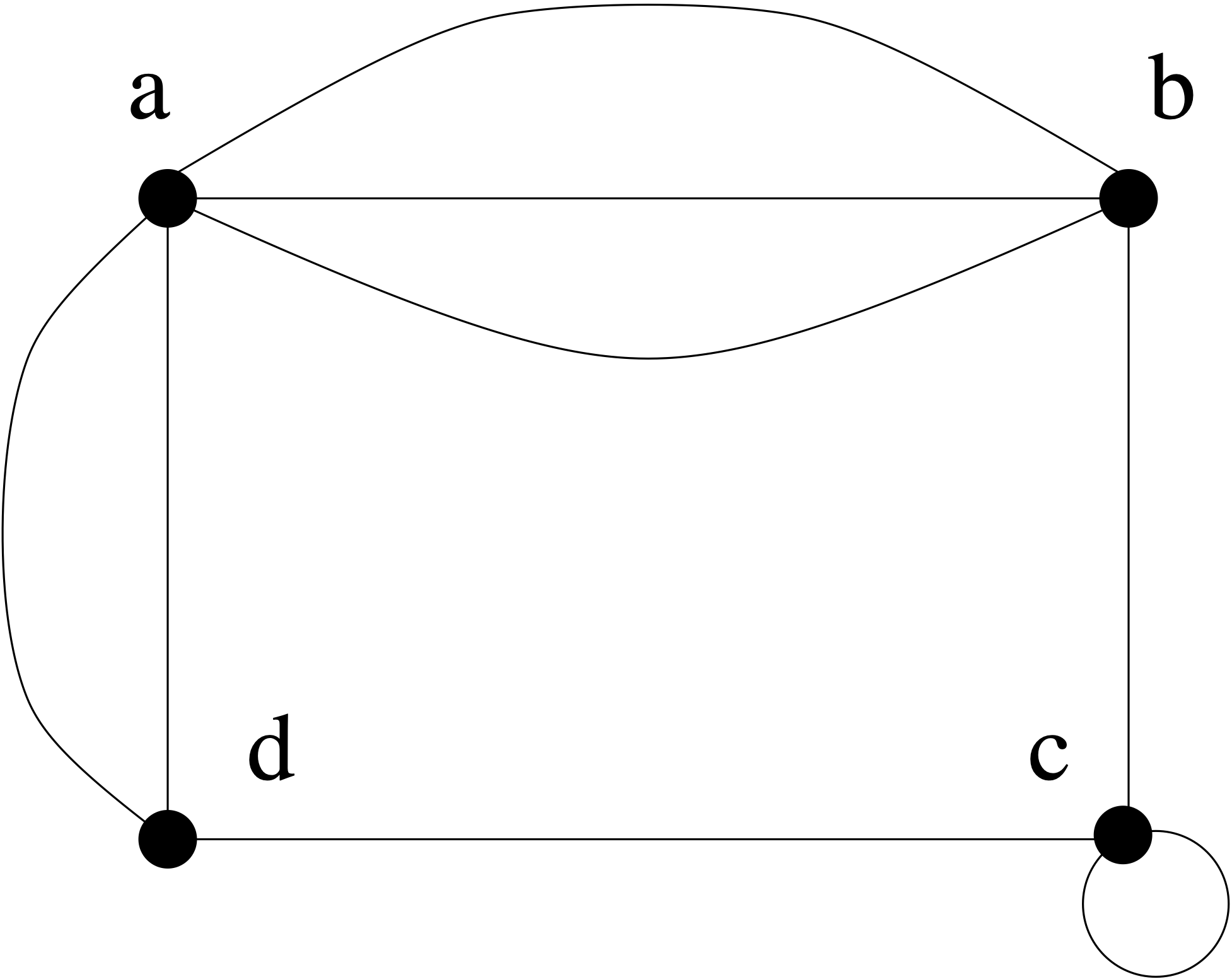
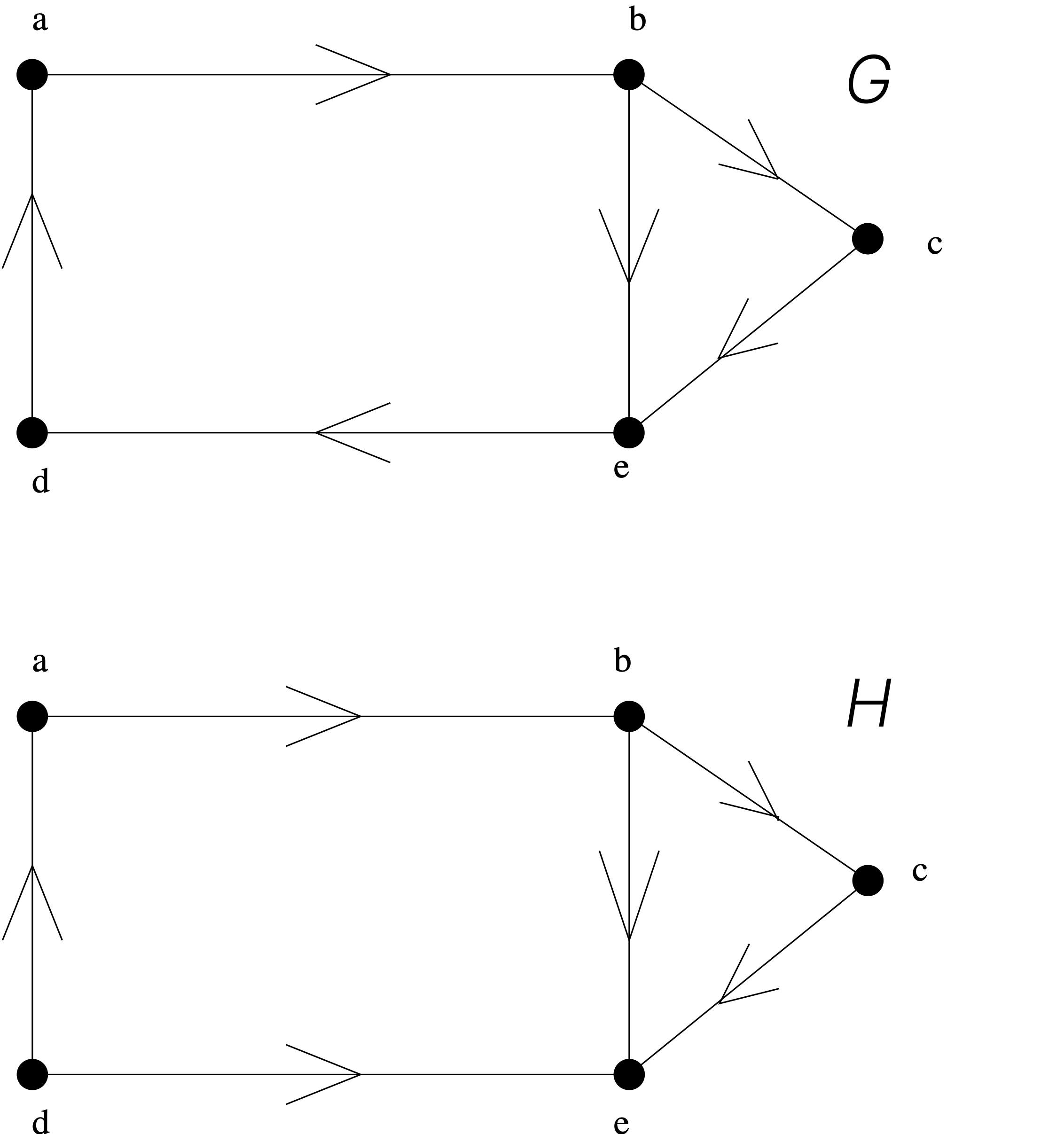
Example 5.27 Are the directed graphs and shown below strongly connected? Are they weakly connected?
Isomorphism of graphs
We often need to know whether it is possible to draw two graphs in the same way. For instance, in chemistry, graphs are used to model compounds. Different compounds can have the same molecular formula but can differ in structure. Such compounds will be represented by graphs that cannot be drawn in the same way. The graphs representing previously known compounds can be used to determine whether a supposedly new compound has been studied before.
Isomorphic graphs
Link copiedDefinition 5.20 The simple graphs and are isomorphic if there is a one-to-one and onto function with the property that and are adjacent in if and only if and V2” /> with the property that and are adjacent in if and only if are adjacent in , for all and in . Such a function is called an_ isomorphism.
In other words, when two simple graphs are isomorphic, there is a one-to-one correspondence between vertices of the two graphs that preserves the adjacency relationship.
Invariant properties
Link copiedIt is often difficult to determine whether two simple graphs are isomorphic. There are possible one-to-one correspondences between the vertex sets of two simple graphs with vertices. Testing each such correspondence to see whether it preserves adjacency and nonadjacency is impractical if is at all large.
However, we can often show that two simple graphs are not isomorphic by showing that they do not share a property that isomorphic simple graphs must both have. Such a property is called an invariant with respect to isomorphism of simple graphs. For instance:
- Isomorphic simple graphs must have the same number of vertices, since there is a one-to-one correspondence between the sets of vertices of the graphs.
- Isomorphic simple graphs must have the same number of edges, because the one-to-one correspondence between vertices establishes a one-to-one correspondence between edges.
- The degrees of the vertices in isomorphic simple graphs must be the same. That is, a vertex of degree in must correspond to a vertex of degree in , since a vertex in is adjacent to if and only if and are adjacent in . In other words, two isomorphic graphs should have the same degree sequence.
Number of vertices and edges in isomorphic graphs
Link copiedThe number of vertices, the number of edges, and the degrees of the vertices are all invariants under isomorphism. If any of these quantities differ in two simple graphs, these graphs cannot be isomorphic.
However, when these invariants are the same, it does not necessarily mean that the two graphs are isomorphic. There are no useful sets of invariants currently known that can be used to determine whether simple graphs are isomorphic.
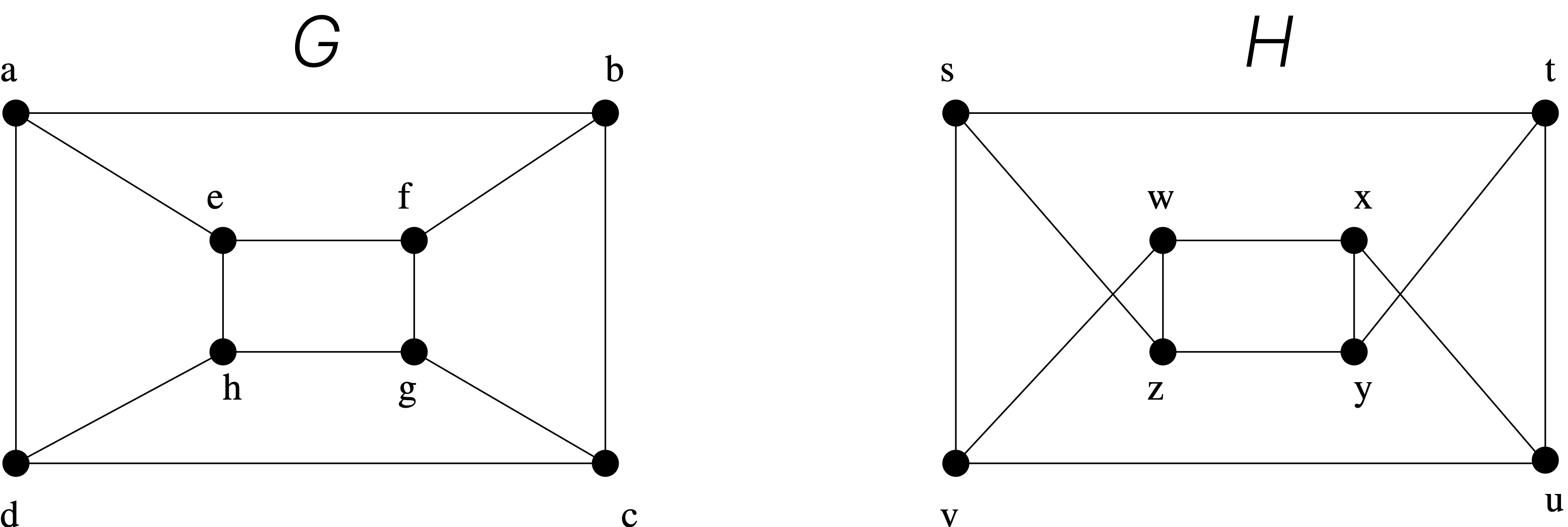
To show that a function from the vertex set of a graph to the vertex set of a graph is an isomorphism, we need to show that preserves edges.
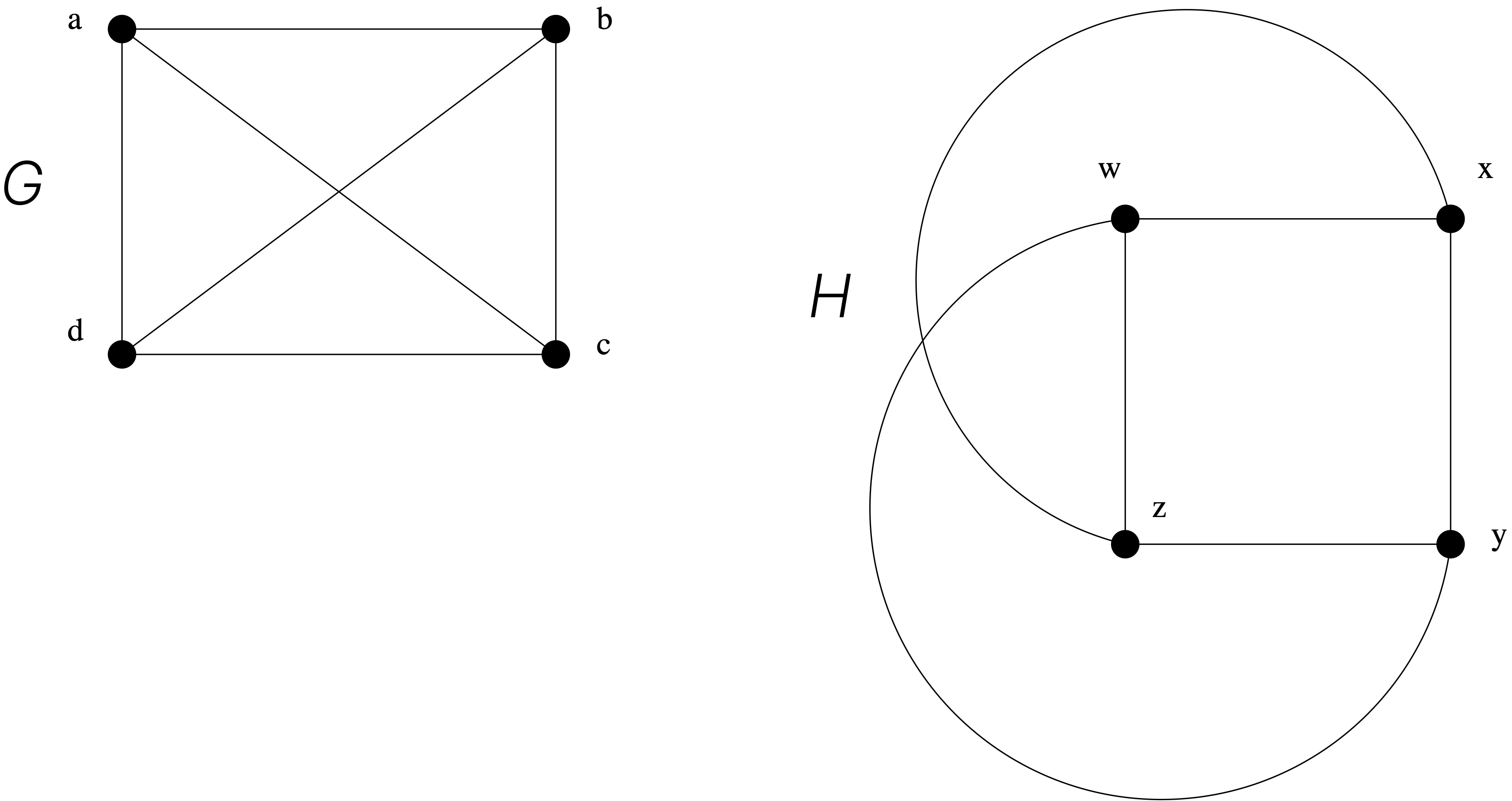
Paths and isomorphism
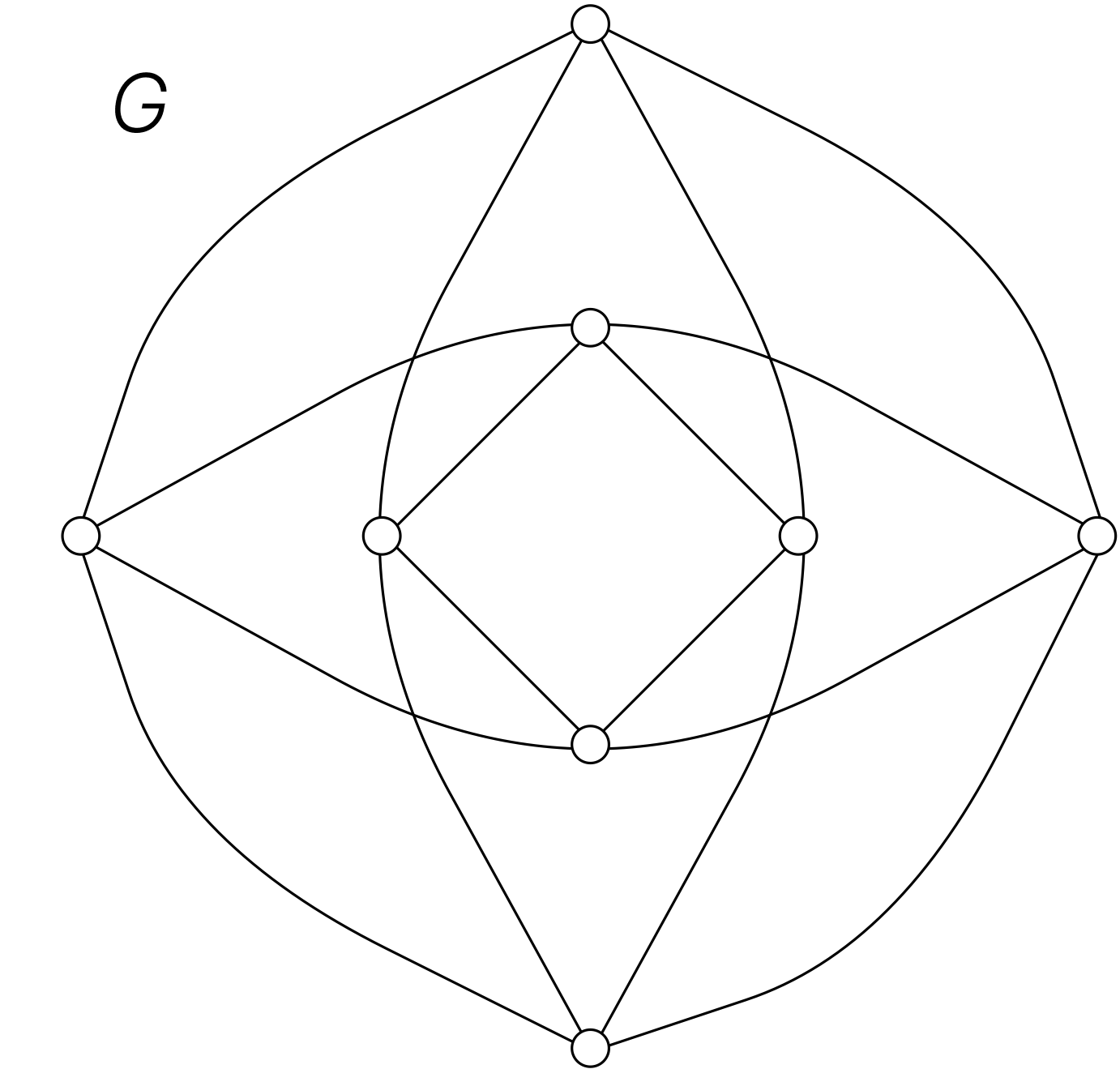
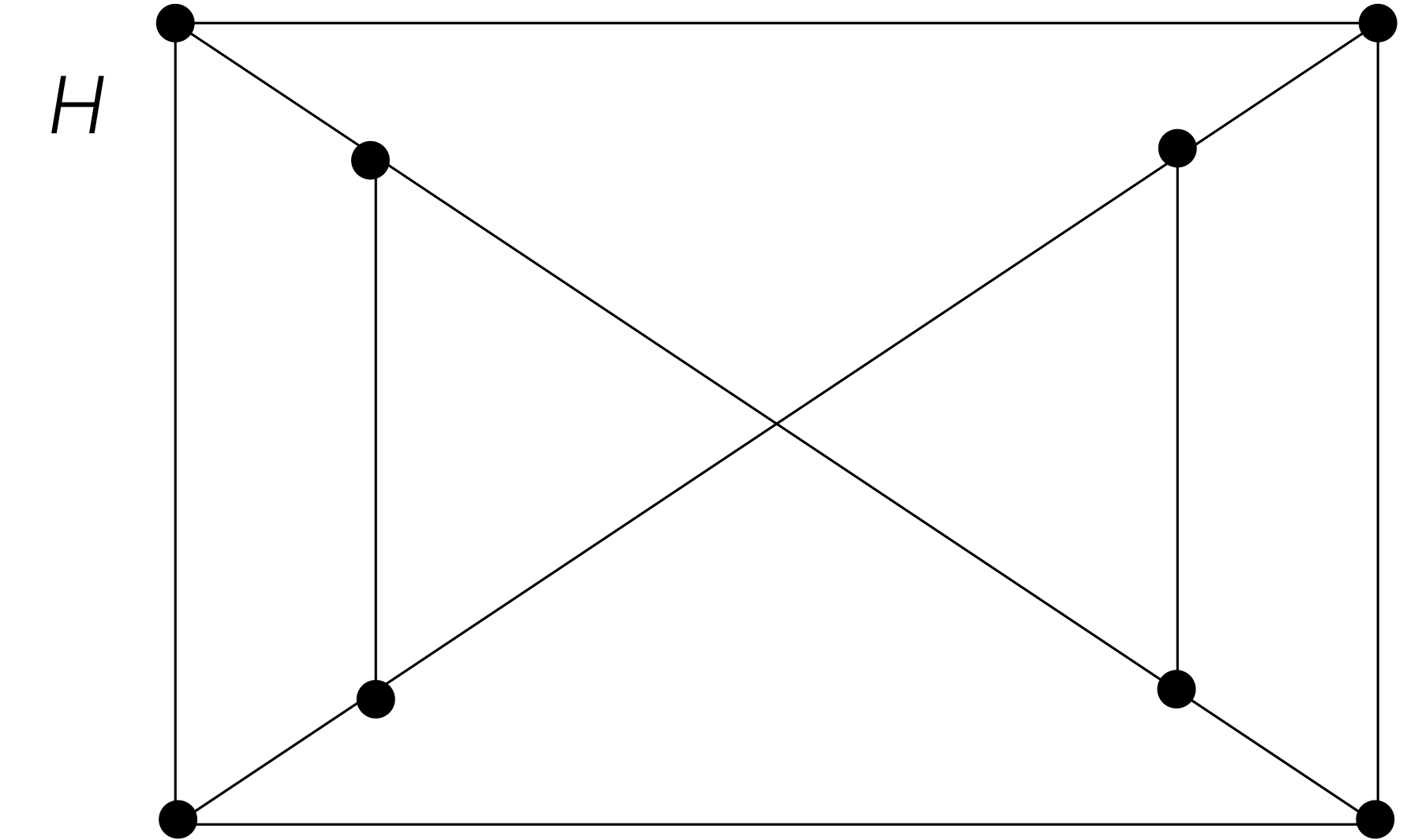
Link copiedThere are several ways that walks and cycles can help determine whether two graphs are isomorphic. For example, the existence of a cycle of a particular length is a useful invariant that can be used to show that two graphs are not isomorphic. In addition, walks can be used to construct mappings that may be isomorphisms.
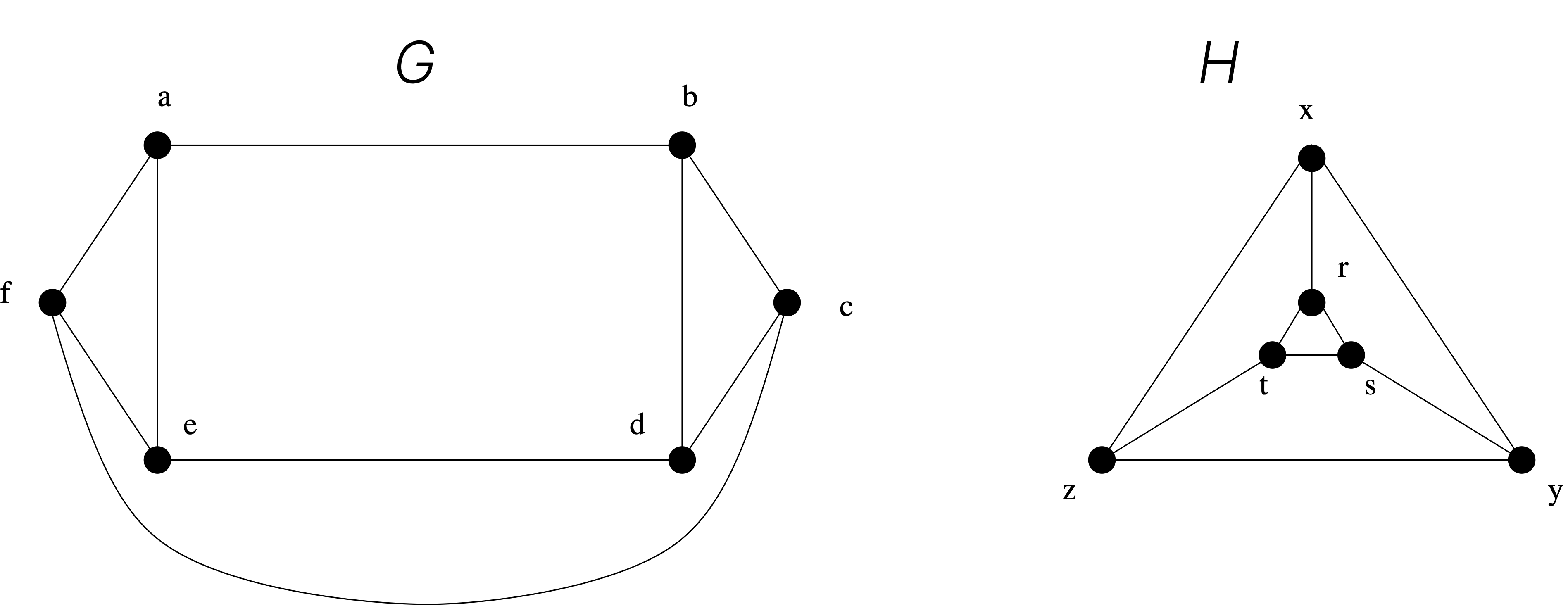
We have shown how the existence of a type of walk, namely, a cycle of a particular length, can be used to show that two graphs are not isomorphic. We can also use walks to find mappings that are potential isomorphisms.
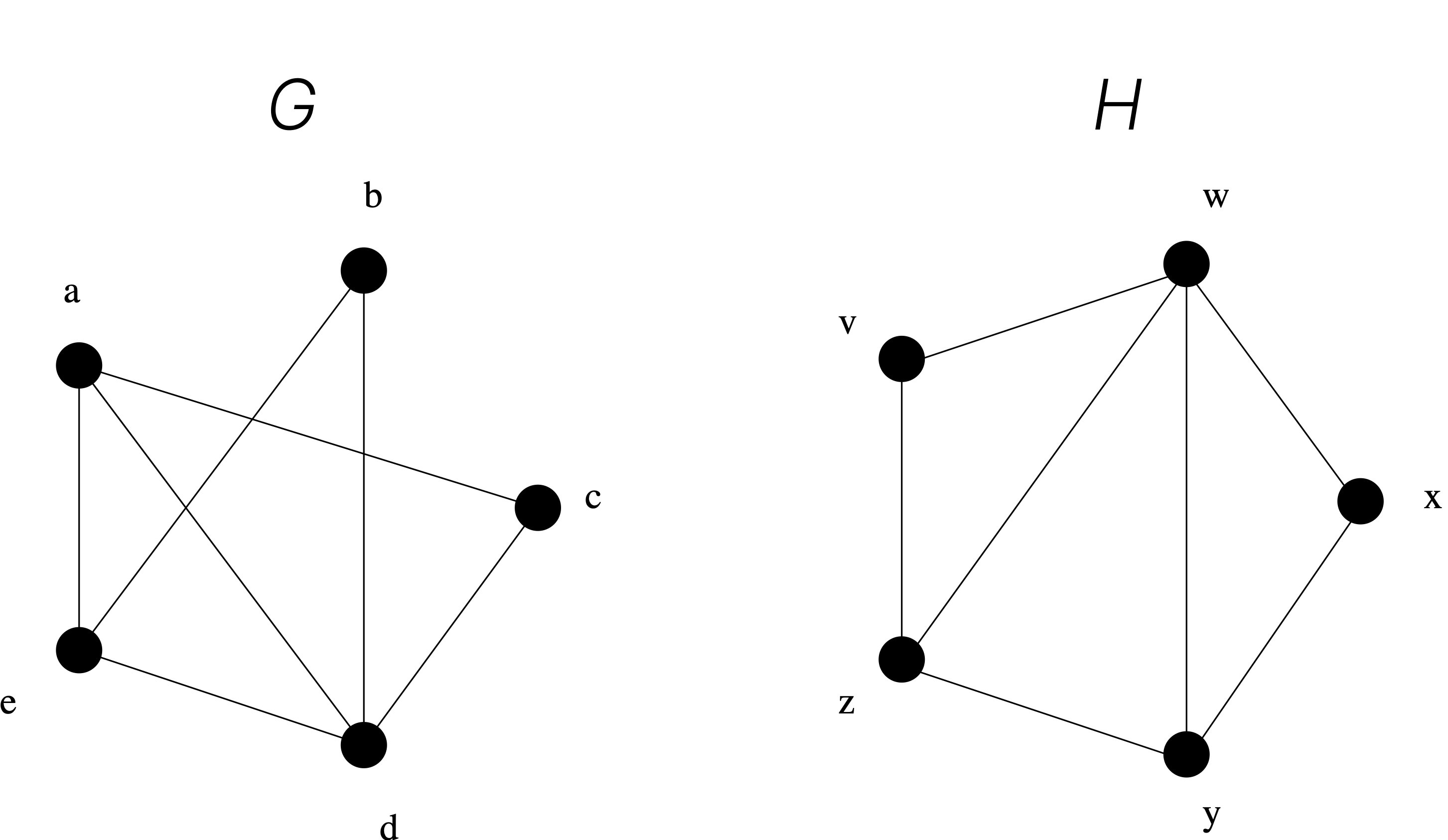
Euler circuits and walks
We now tell a famous story in the history of graph theory. Back in the 18th century, the town of Königsberg was part of Prussia (it is now called Kaliningrad and is part of the Russian republic). The town was divided into four sections by the Pregel River. These four sections included the two regions on the banks of the Pregel, Kneiphof Island, and the region between the two branches of the Pregel. In the 18th century seven bridges connected these regions. The image below (from the MacTutor website) depicts these regions and bridges.
The people in the town enjoyed walking through the town on Sundays. They wondered whether it was possible to start at some location in the town, travel across all the bridges without crossing any bridge twice, and return to the starting point.
The Swiss mathematician Leonhard Euler showed that no such Sunday stroll exists. His solution was published in 1736, and is considered to be the birth of graph theory. Euler studied this problem using the multigraph obtained when the four regions are represented by vertices and the bridges are represented by edges. This multigraph is shown below.
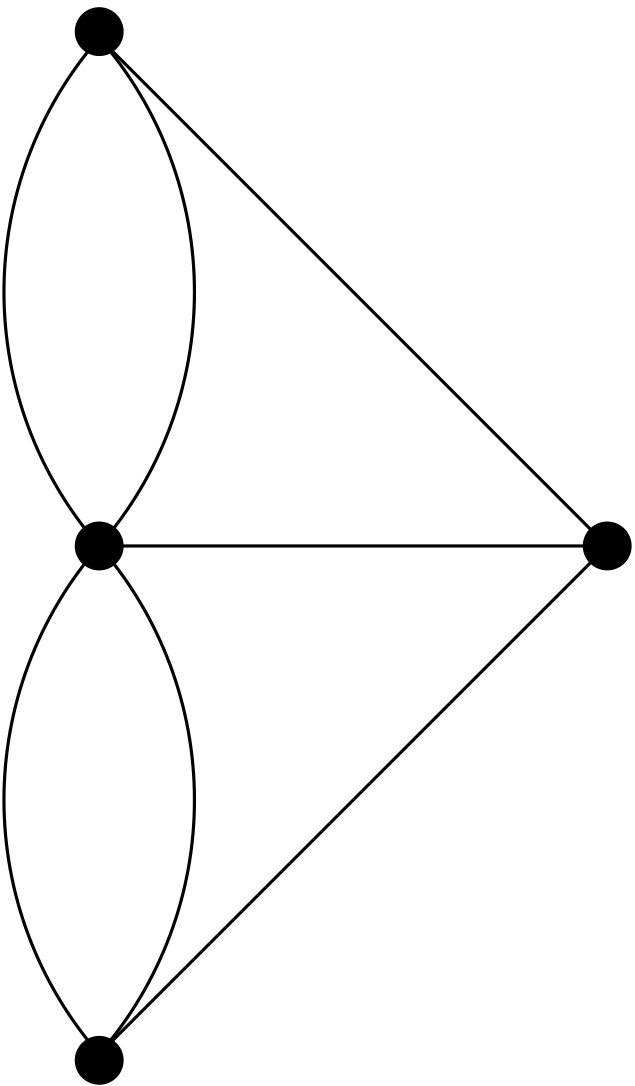
Euler circuit and walks
Link copiedThe problem of traveling across every bridge without crossing any bridge more than once can be rephrased in terms of this model. The question becomes: Is there a circuit in this multigraph that contains every edge exactly once? (Note that this circuit is required to visit every edge, so it must visit vertices of degree more than once.) This may seem an artificial problem, but it has applications in scheduling postal delivery routes and trash collection services.
Definition 5.21 An Euler circuit in a graph is a circuit containing every edge of exactly once. An Euler walk in is a walk containing every edge of exactly once.


Necessary and sufficient condition for Euler circuits
Link copiedThere are simple criteria for determining whether a multigraph has an Euler circuit or an Euler walk. Euler discovered them when he solved the famous Königsberg bridge problem. We will assume that all graphs discussed in this section have a finite number of vertices and edges.
What can we say if a connected multigraph has an Euler circuit? What we can show is that every vertex must have even degree.
- To do this, first note that an Euler circuit begins with a vertex and continues with an edge incident to , say . The edge contributes 1 to .
- Each time the circuit passes through a vertex it contributes 2 to the vertex’s degree, since the circuit enters via an edge incident with this vertex and leaves via another such edge.
- Finally, the circuit terminates where it started, contributing 1 to . Therefore, must be even, because the circuit contributes 1 when it begins, 1 when it ends, and 2 every time it passes through (if it ever does).
- A vertex other than has even degree because the circuit contributes 2 to its degree each time it passes through the vertex.
- We conclude that if a connected graph has an Euler circuit, then every vertex must have even degree.
Is this necessary condition for the existence of an Euler circuit also sufficient? That is, must an Euler circuit exist in a connected multigraph if all vertices have even degree? The next result is one of the first big theorems in graph theory.
Theorem 5.8 A connected multigraph has an Euler circuit if and only if each of its vertices has even degree.
The algorithm below gives the constructive procedure for finding Euler circuits.
procedure ( connected multigraph with all vertices of even degree)
a circuit in beginning at an arbitrarily chosen vertex with edges successively added to form a walk that returns to this vertex.
with the edges of removed
while has edges
begin
- a circuit in beginning at a vertex in that also is an endpoint of an edge of
- with edges of and all isolated vertices removed
- with inserted at the appropriate vertex
end is an Euler circuit
Necessary and sufficient condition for Euler walks
Link copiedTheorem 5.9 A connected multigraph has an Euler walk but not an Euler circuit if and only if it has exactly two vertices of odd degree.
Hamilton paths and cycles
We have developed necessary and sufficient conditions for the existence of walks and circuits that contain every edge of a multigraph exactly once. Can we do the same for walks and circuits that contain every vertex of the graph exactly once?
Definition 5.22 A path in the graph is called a Hamilton path if
A cycle
(with ) in a graph is called a Hamilton cycle if is a Hamilton path.
Hamilton's puzzle
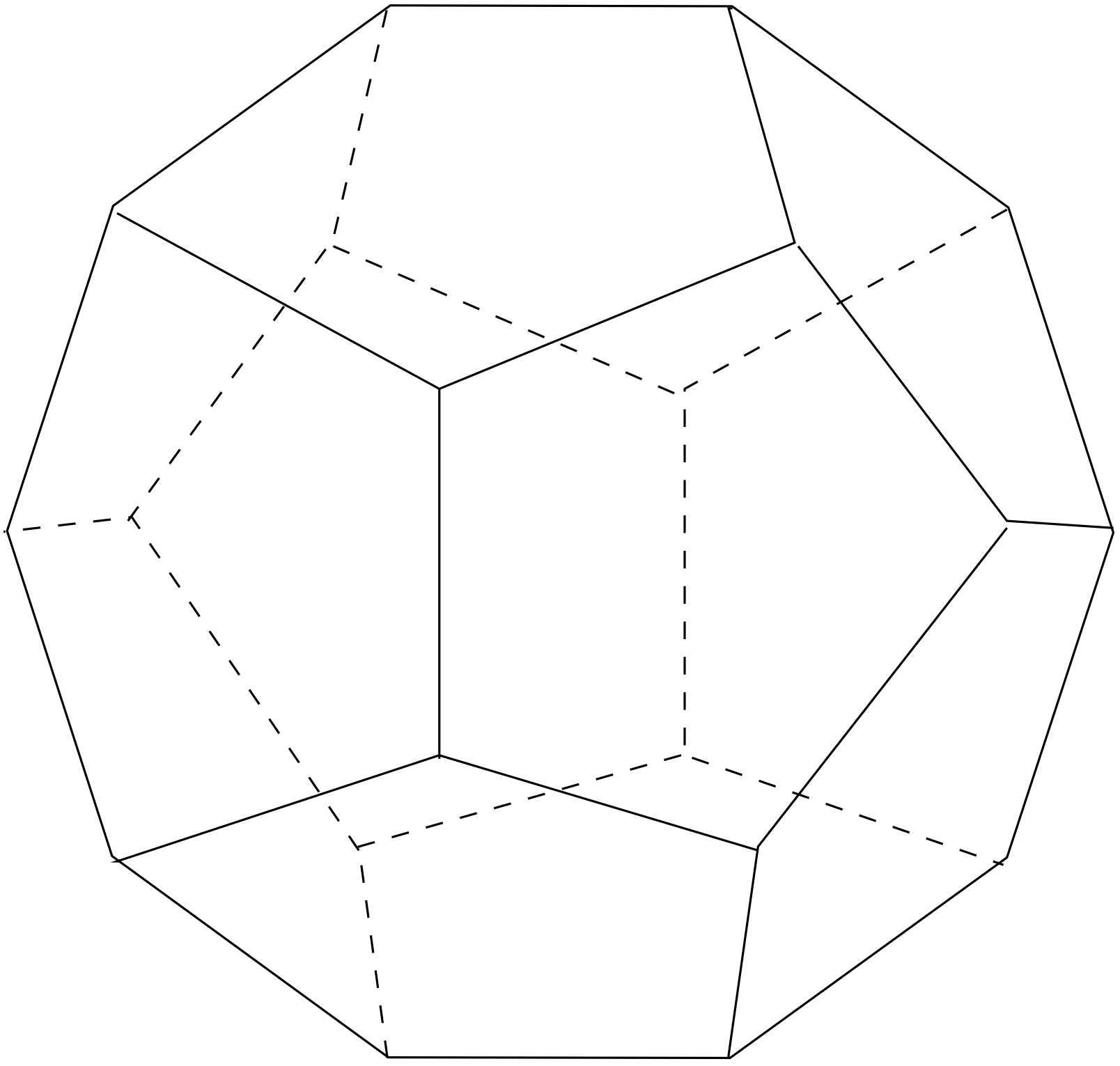
Link copiedThis terminology comes from a puzzle invented in 1857 by the Irish mathematician Sir William Rowan Hamilton. Hamilton’s puzzle consisted of a wooden dodecahedron (a polyhedron with 12 regular pentagons as faces, as shown below, with a peg at each vertex of the dodecahedron, and string). The 20 vertices of the dodecahedron were labeled with different cities in the world. The object of the puzzle was to start at a city and travel along the edges of the dodecahedron (see the following picture), visiting each of the other 19 cities exactly once, and end back at the first city. The circuit traveled was marked off using the strings and pegs.
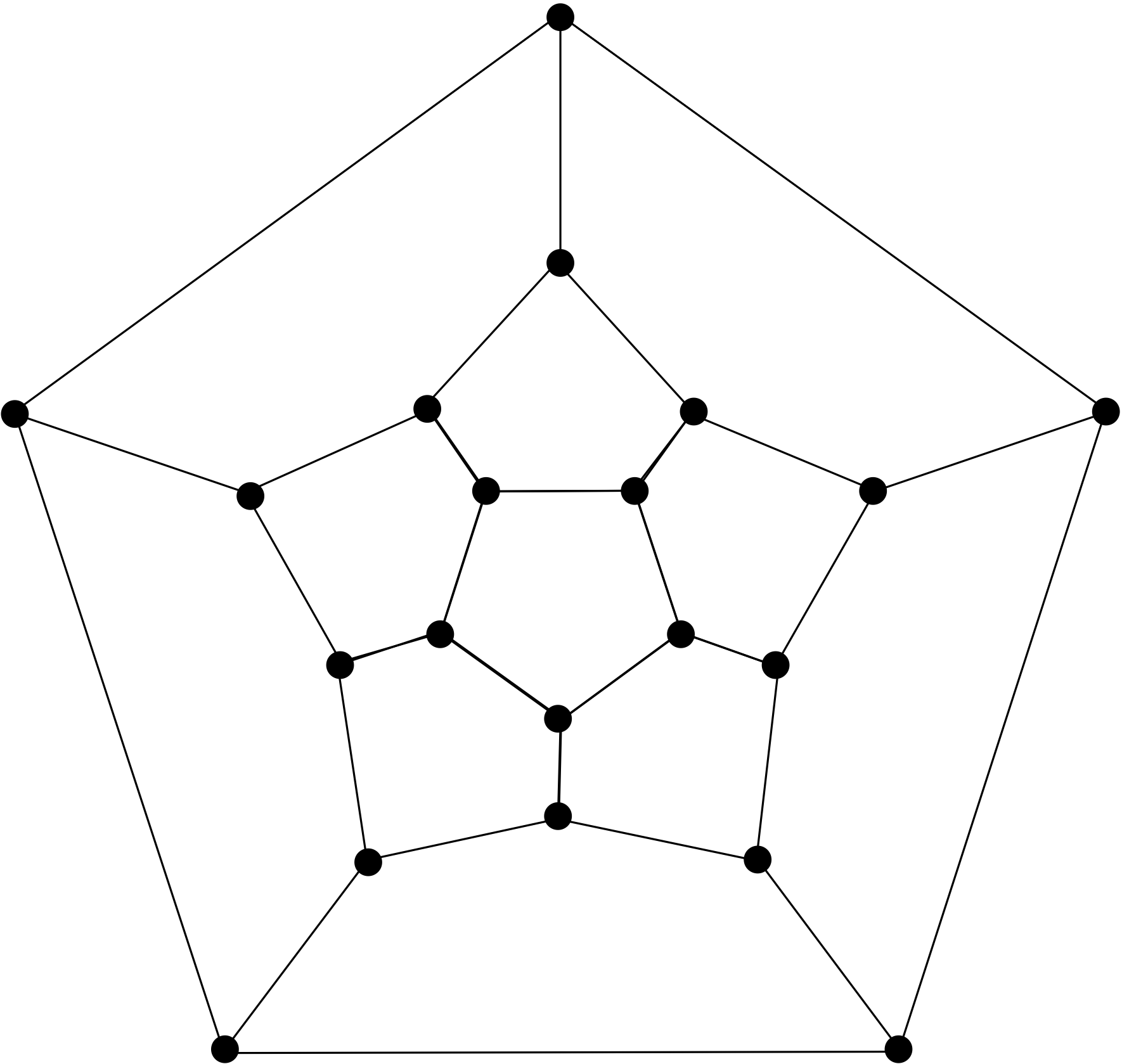

Determining whether a graph contains a Hamilton cycle
Link copiedIs there a simple way to determine whether a graph has a Hamilton cycle or path? At first, it might seem that there should be an easy way to determine this, since there is a simple way to answer the similar question of whether a graph has an Euler circuit.
Surprisingly, there are no known simple necessary and sufficient criteria for the existence of Hamilton cycles. However, many theorems are known that give sufficient conditions for the existence of Hamilton cycles. Also, certain properties can be used to show that a graph has no Hamilton cycle.
- A graph with a vertex of degree 1 cannot have a Hamilton cycle, since in a Hamilton cycle each vertex is incident with two edges in the circuit.
- If a vertex in the graph has degree 2, then both edges that are incident with this vertex must be part of any Hamilton cycle.
- When a Hamilton cycle is being constructed and this circuit has passed through a vertex, then all remaining edges incident with this vertex, other than the two used in the circuit, can be removed from consideration.
- A Hamilton cycle cannot contain a smaller circuit within it.

The traveling salesperson problem
Link copiedSuppose the drawing below is a map showing four cities and the distances in kilometers between them. Suppose that a salesperson must visit each city exactly once, starting and ending in city A. Which route from city to city will minimize the total distance that must be traveled?
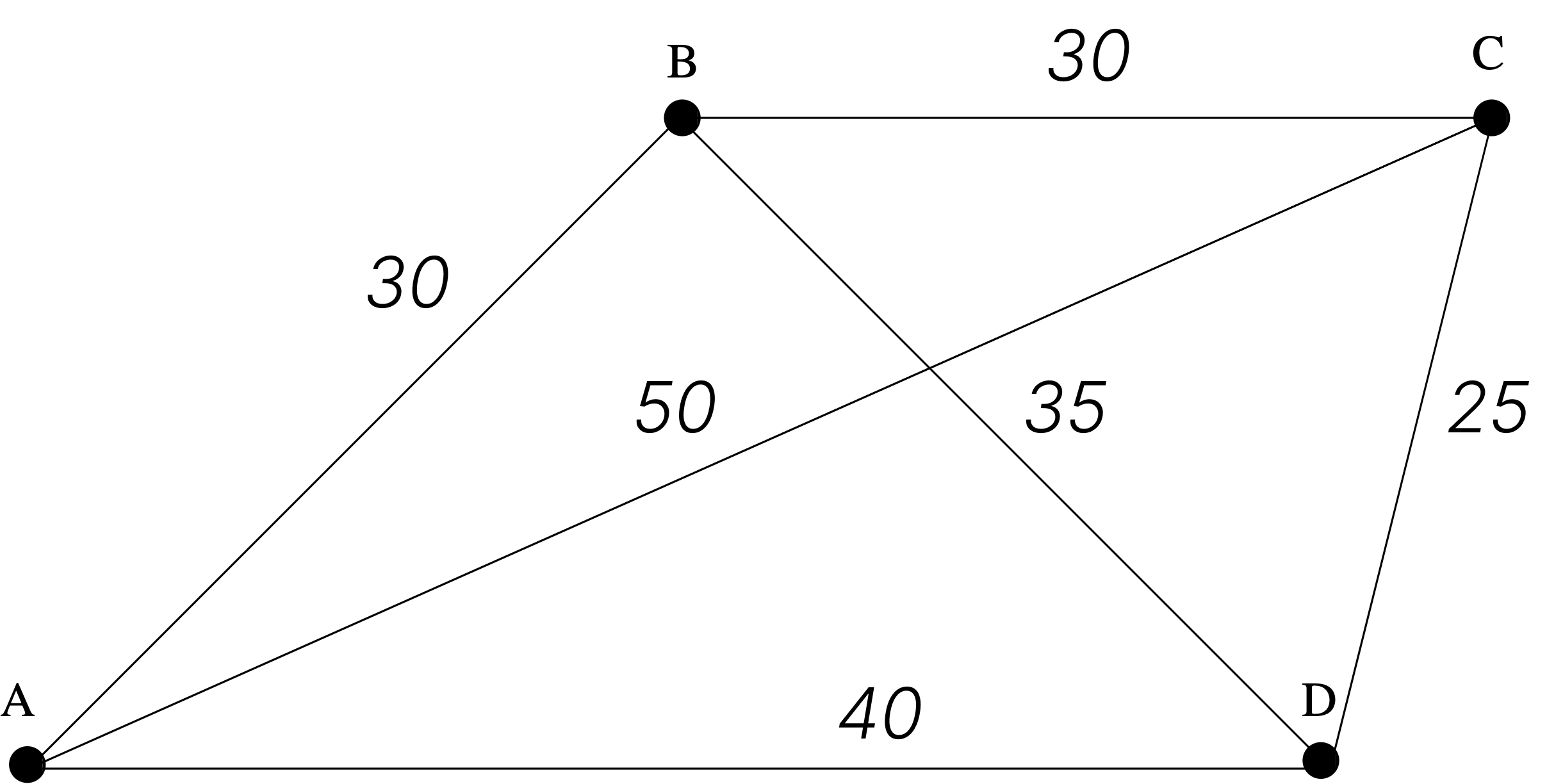
This problem can be solved by writing all possible Hamiltonian circuits starting and ending at A and calculating the total distance traveled for each.
Thus either route ABCDA or ADCBA gives a minimum total distance of 125 kilometers.
The general traveling salesperson problem involves finding a Hamiltonian circuit to minimize the total distance traveled for an arbitrary graph with vertices in which each edge is marked with a distance. One way to solve the general problem is to use the above method. Write down all Hamiltonian circuits starting and ending at a particular vertex, compute the total distance for each, and pick one for which this total is minimal. However, even for medium-sized values of this method is impractical. At present, there is no known algorithm for solving the general traveling salesperson problem that is more efficient. However, there are efficient algorithms that find ‘pretty good’ solutions, that is, circuits that, while not necessarily having the least possible total distance, have smaller total distances than most other Hamiltonian circuits.