Deterministic Finite Automata

Alphabet and strings

Let $\Sigma$ be a finite alphabet. When $\Sigma$ contains $k$ letters, we say $\Sigma$ is a $k$ -letter alphabet. A 1-letter alphabet is a unary alphabet, and a 2-letter alphabet is a binary alphabet. Our typical binary alphabet is $\{a,b\}$ . A finite sequence of symbols from $\Sigma$ is called a string or word.

Each string $v$ is of the form $\sigma_1 \sigma_2 \ldots \sigma_n,$ where $\sigma_i\in\Sigma$ . The length of $v$ , denoted by $|v|$ , is the number of symbols it has. Thus, $|abb|=3$ , $|baba|=4$ , and $|a|=1$ .

The string of length $0$ is called the empty string. It is denoted $\lambda$ .

There are $k^n$ strings of length $n$ over a $k$ -letter alphabet.

The set of all strings over the alphabet $\Sigma$ is

We denote strings by the letters $u,v,w, \ldots$ .

The concatenation of $u$ and $v$ is obtained by writing $u$ followed by $v$ . Concatenation is denoted by $u\cdot v$ . We have:

Note that for any string $u$ , because $\lambda$ is the empty string, we have $\lambda \cdot u =u\cdot \lambda = u$ .

We sometime write $uv$ , instead of $u\cdot v$ .

For a string $u$ we denote by $u^n$ the following string:

If a string $w$ occurs in a string $u$ , we say that $w$ is a substring of $u$ . That is, $w$ is a substring of $u$ if $u=u_1wu_2$ for some strings $u_1$ and $u_2$ . One can see that every string $u$ is a substring of itself (take $u_1 = u_2 = \lambda$ ).

A string $w$ is a prefix of a string $u$ if $u$ can be written as $wu_1$ .

For example, The prefixes of $aabbba$ are $\lambda$ , $a$ , $aa$ , $aab$ , $aabb$ , $aabbb$ and $aabbba$ .

A language over an alphabet $\Sigma$ is a subset of $\Sigma^{\star}$ .

Here are some examples of languages:

1. $\emptyset$ , $\Sigma^\star$ , $\{a^n \mid n\in \N \}$ , $\{aba, bab\}$ .
2. $\{w \in \{a,b\}^\star \mid bab$ is a substring of $w\}$ .
3. $\{w \in \Sigma^\star \mid w$ has even length $\}$ .
4. $\{w \in \Sigma^\star \mid w$ has a substring $aba\}$ .

We denote languages by $U$ , $V$ , $W$ , $L$ , $\ldots$ .

Operations on languages

Let $U$ and $V$ be languages over an alphabet $\Sigma$ . The following operations on languages are called Boolean operations:

1. The union of $U$ and $V$ is $U\cup V$ ,
2. The intersection of $U$ and $V$ is $U\cap V$ ,
3. The complement of $U$ is $\Sigma^{\star}\setminus U$ .

Let $U$ and $W$ be languages on some alphabet set $\Sigma$ . The concatenation of $U$ and $W$ , denoted by $U\cdot W$ , is the language $U\cdot W =\{u\cdot w \mid u\in U, w\in W\}$ .

Let $U$ be a language over an alphabet $\Sigma$ . Suppose we are given a string $v$ , and we would like to check whether $v$ belongs to $U$ . A deterministic finite automaton (DFA) is an algorithm that determines whether $v$ belongs to $U$ or not.

We can represent a finite automata as a labeled directed graph. We call this graph the transition diagram.

Definition 7.1 _A deterministic finite automaton (DFA) is a $5$ -tuple $(S, q_0, T, F, \Sigma)$ , where

• $S$ is the set of states.
• $T$ is the transition function $T:S\times \Sigma \rightarrow S$ .
• $F$ is a subset of $S$ called the set of accepting states.
• $\Sigma$ is an alphabet.
• $q_0$ is the initial state. Note that $q_0\in S$ .

Example 7.2 Let us look at the language $U$ that consists of all strings $u$ such that $u$ contains the substring $baa$ . We want to design an algorithm that, given a string $v$ , determines whether $v\in U$ . Below is the $Find$ -$baa(v)$ -algorithm that on input

determines if $v$ contains $baa$ as a sub-string (and if it does, then $v \in U$ ).

Find-baa(v)-algorithm

The algorithm makes its transitions from one state to another depending on the input symbol $\sigma$ read. The transition function is $T : \{ 0,1,2,3\} \times \{ a, b\} \to \{ 0,1,2,3 \}$ given by the following Table.

We can represent a finite automata as a labeled directed graph. We call this graph transition diagram. Therefore we have the following transition diagram for the $Find$ -$baa(v)$ -algorithm.

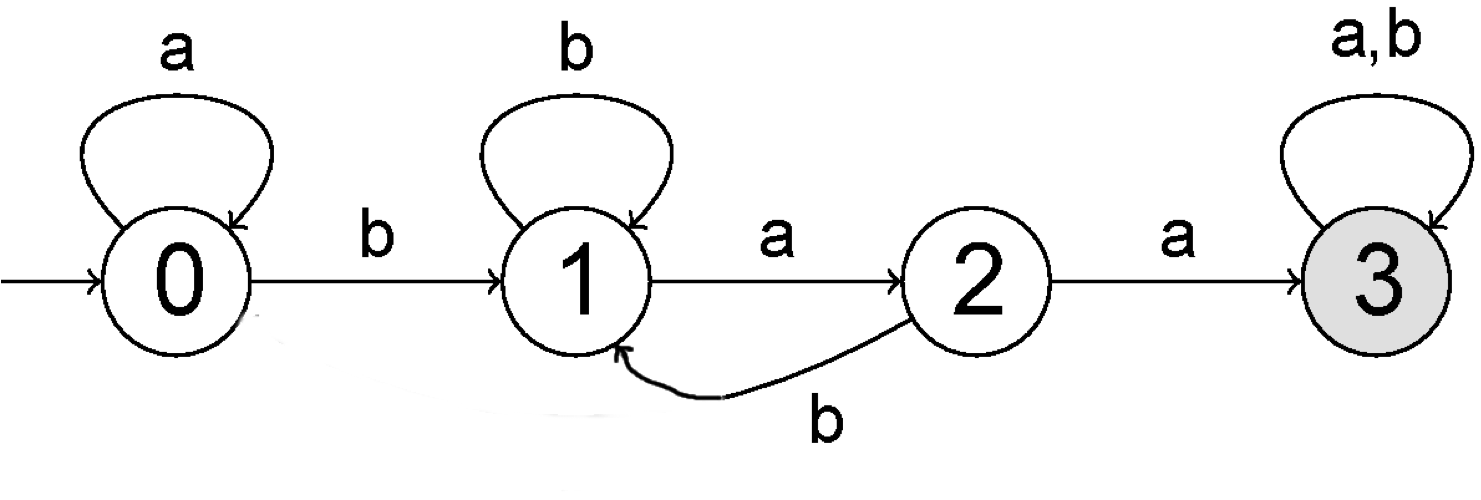
As a program, the algorithm Find-baa is the following:

1. Initialize variables $i=1$ and $state=0$ .
2. If $state=0$ and $\sigma_i=a$ then set $state=0$ .
3. If $state=0$ and $\sigma_i=b$ then set $state=1$ .
4. If $state=1$ and $\sigma_i=a$ then set $state=2$ .
5. If $state=1$ and $\sigma_i=b$ then set $state=1$ .
6. If $state=2$ and $\sigma_i=a$ then set $state=3$ .
7. If $state=2$ and $\sigma_i=b$ then set $state=1$ .
8. If $state=3$ and $\sigma_i\in \{a,b\}$ then $state=3$ .
9. Increment $i$ by one.
10. If $i=n+1$ then go to Line 11. Otherwise go to Line $2$ .
11. If $state=3$ then output accept. Otherwise output reject.

Let $\mathcal M=(S, q_0, T, F, \Sigma)$ be a DFA and $u=\sigma_1\ldots \sigma_n$ be a string. The run of the automaton on $u$ is the sequence of states $s_1, s_2, \ldots,s_n, s_{n+1}$ such that $s_1$ is the initial state and $T(s_i, \sigma_i)=s_{i+1}$ for all $i=1,\ldots, n$ .

The run of $\mathcal M$ on a string $u=\sigma_1\ldots \sigma_n$ can be viewed of as the execution the following algorithm $Run(\mathcal M, u)$ :

1. Initialize $s=q_0$ , $i=1$ , and print $s$ .
2. While $i\leq n$ do

(a) Set $\sigma=\sigma_i$ .

(b) Set $s=T(s,\sigma)$ .

(c) Print $s$ .

(d) Increment $i$

Let $\mathcal M=(S, q_0, T, F, \Sigma)$ be a DFA and $u=\sigma_1\ldots \sigma_n$ be a string. We say that $\mathcal M$ accepts $u$ if the run $s_1,\ldots, s_n, s_{n+1}$ of $\mathcal M$ on $u$ is such that the last state $s_{n+1}\in F$ . Such a run is called an accepting run.

Let $\mathcal M=(S,q_0, T,F,\Sigma)$ be a DFA. The language accepted by $\mathcal M$ , denoted by $L(\mathcal M)$ , is the language $L(\mathcal M) = \{w \mid$ the automaton $\mathcal M$ accepts $m\}$ .

A language $L\subseteq \Sigma^\star$ is DFA recognizable if there exists a DFA $\mathcal M$ such that $L=L(\mathcal M)$ .

Example 7.4 Consider a DFA with exactly one state. If the state is an accepting state, then the automaton accepts the language $\Sigma^\star$ . If the state is not an accepting state, then the automaton recognizes the empty language $\emptyset$ .

This language $L$ is recognized by the following DFA $(S, 0, T, F)$ :

1. $S=\{0,1,2,3,4,\ldots, n+1\}$ with $0$ being the initial state.

2. For all $i \leq n-1$ , $T(i,\sigma_{i+1})=i+1$ . In other cases $T(s,\sigma)=n+1$ .

3. The accepting state is $n$ .

Designing finite automata

Given a language $L$ , we would like design a deterministic finite automata that recognizes the language $L$ . But can we always do so? And if so, how?

For example, let us consider the language $L=\{ ab^na \mid n \in \N \}$ . Is there a DFA recognising $L$ ?

Our problem is to design a DFA recognizing this language.

One way of doing so, is to count the number of $a$ ‘s and $b$ ‘s in each given word. But we don’t really need to count the number of $a$ ‘s and $b$ ‘s. We just need to keep track of four cases: whether the number of $a$ ‘s is odd or even, and whether the number of $b$ ‘s is odd or even. We can do this with four states:

State 0: Even number of $a$ ‘s and $b$ ‘s.

Stete 1: Even number of $a$ ‘s and odd number of $b$ ‘s .

State 2: Odd number of $a$ ‘s and $b$ ‘s.

State 3: Odd number of $a$ ‘s and even number of $b$ ‘s.

We get the following transition diagram:

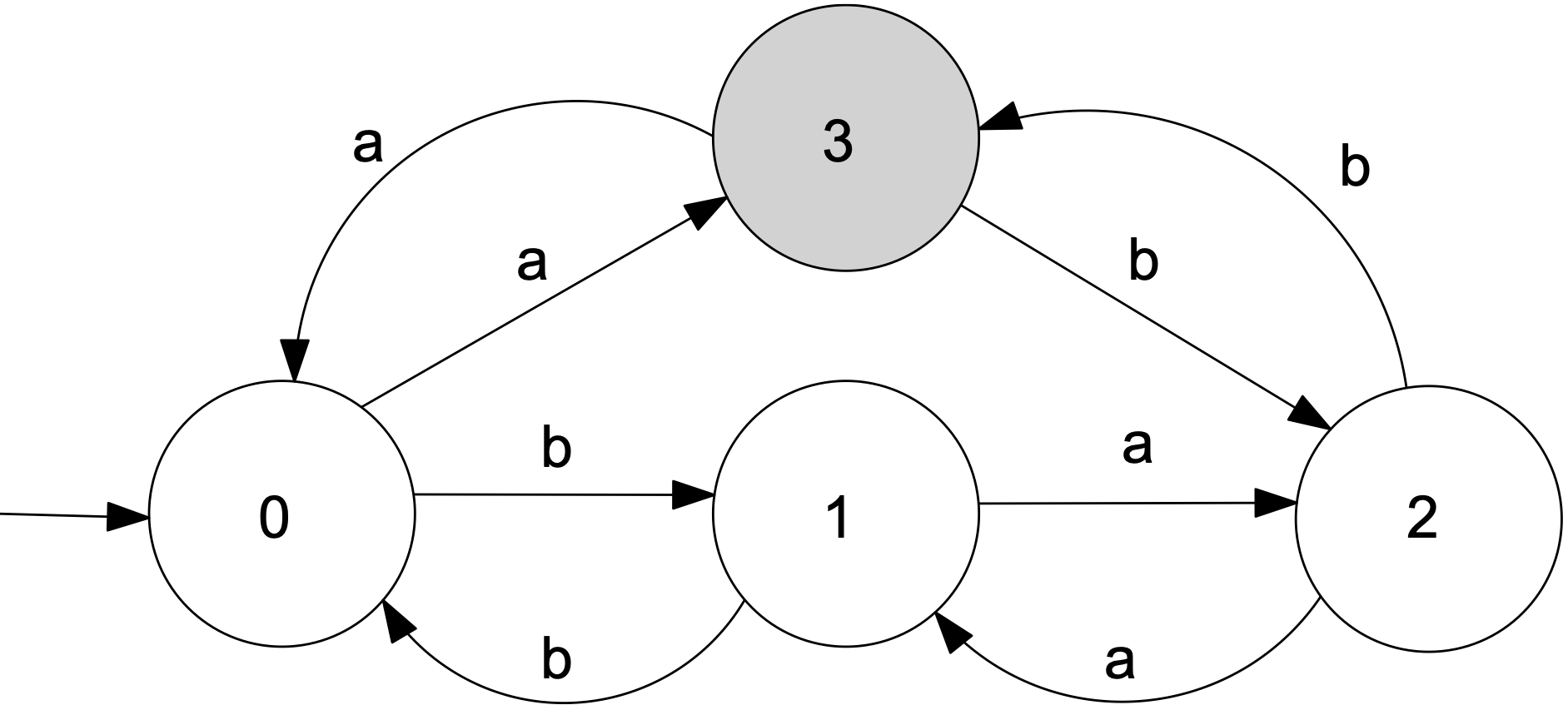
Designing finite automata

Let $\mathcal M_1=(S_1, q_0^{(1)}, T_1,F_1)$ and $\mathcal M_2=(S_2, q_0^{(2)}, T_2, F_2)$ , and let two DFA recognizing $L_1=L(\mathcal M_1)$ and $L_2=L(\mathcal M_2)$ .

The Union Problem: Design a DFA $\mathcal M=(S, q_0, T,F)$ that recognizes $L_1\cup L_2$ .

Construction of DFA $\mathcal M=(S,q_0, T, F)$ for $L_1\cup L_2$

1. The set $S$ of states is $S_1\times S_2$ .

2. The initial state is the pair $(q_0^{(1)}, q_0^{(2)})$ .

3. The transition function $T$ is the product of the transition functions $T_1$ and $T_2$ , that is:

where $p\in S_1$ , $q\in S_2$ , and $\sigma \in \Sigma$ .

4. The set $F$ of final states consists of all pairs $(p,q)$ such that either $p\in F_1$ or $q\in F_2$ .

The notation for the new automaton is: $\mathcal M_1\oplus \mathcal M_2$ .

If $u\in L_1\cup L_2$ then either $M_1$ accepts $u$ or $M_2$ accepts $u$ . In either case, since $M$ simulates both $M_1$ and $M_2$ , the string $u$ must be accepted by $M$ .

If $u$ is accepted by $M$ then the run of $M$ on $u$ is split into two runs: one is the run of $M_1$ on $u$ and the other is the run of $M_2$ on $u$ . Since $M$ accepts $u$ , it must be the case that one of the runs is accepting.

Let $\mathcal M_1=(S_1, q_0^{(1)}, T_1,F_1)$ and $\mathcal M_2=(S_2, q_0^{(2)}, T_2, F_2)$ , and let two DFA recognizing $L_1=L(\mathcal M_1)$ and $L_2=L(\mathcal M_2)$ .

The intersection problem : Design a DFA $\mathcal M=(S, q_0, T,F)$ that recognizes $L_1\cap L_2$ .

Construction of DFA $\mathcal M=(S,q_0, T, F)$ for $L_1\cap L_2$

1. The set $S$ of states is $S_1\times S_2$ .

2. The initial state is the pair $(q_0^{(1)}, q_0^{(2)})$ .

3. The transition function $T$ is the product of the transition functions $T_1$ and $T_2$ , that is:

where $p\in S_1$ , $q\in S_2$ , and $\sigma \in \Sigma$ .

4. The set $F$ of final states consists of all pairs $(p,q)$ such that $p\in F_1$ and $q\in F_2$ .

The notation for the automaton $M$ is this: $M_1\otimes M_2$ .

The complementation problem :

Given a DFA $M=(S,q_0, T, F)$ , design a DFA that recognizes the complement of $L(M)$ .

This is a simple procedure. Keep the original states, the initial state, and the transition function $T$ . Swap: Declare non-accepting states as accepting, and accepting states non-accepting.