Codes

Prefix codes and optional binary trees

To represent symbols, computers use strings of 0’s and 1’s called codewords. For example, in the ASCII (American Standard Code for Information Interchange) code, the letter A is represented by the codeword 01000001, B by 01000010, and C by 01000011. In this system each symbol is represented by some string of eight bits, where a bit is either a 0 or a 1. To translate a long string of 0’s and 1’s into its ASCII symbols we use the following procedure: Find the ASCII symbol represented by the first 8 bits, the ASCII symbol represented by the second 8 bits, etc. For example, 010000110100000101000010 is decoded as CAB.

For many purposes this kind of representation works well. However, there are situations, as in large-volume storage, where this is not an efficient method. In a fixed length representation, such as ASCII, every symbol is represented by a codeword of the same length. A more efficient approach is to use codewords of variable lengths, where the symbols used most often have shorter codewords than the symbols used less frequently. For example, in normal English usage the letters E, T, A, and O are used much more frequently than the letters Q, J, X, and Z.

In this way we have assigned the shortest possible codewords to the most frequently used letters and longer codewords to the other letters. This appears to be a more efficient approach than assigning all these letters a codeword of the same fixed length, which would have to be three or more.

But how can we decode a string of 0’s and 1’s? For example, how should the string 0110110 be decoded? Should we start by looking at only the first digit, or the first two, or the first three? Depending upon the number of digits used, the first letter could be E, O, D or something else. We see that in order to use variable length codewords we need to select representations that permit unambiguous decoding.

A way to do this is to construct codewords so that no codeword is the first part of any other codeword. Such a set of codewords is said to have the prefix property. This property is not enjoyed by the above choice of codewords since the codeword for T is also the first part of the codeword for N. On the other hand, the set of codewords $S = \{000, 001, 01, 10, 11\}$ has the prefix property since no codeword appears as the first part of another codeword. The method to decode a string of 0’s and 1’s into codewords having the prefix property is to read one digit at a time until this string of digits becomes a codeword, then repeat the process starting with the next digit, and continue until the decoding is done.

An efficient method of representation should use codewords such that :

1. the codewords have the prefix property; and

2. the symbols used frequently have shorter codewords than those used less often.

A full binary tree can be used to construct a set of codewords with the prefix property by assigning 0 to each edge from a parent to its left child and 1 to each edge from a parent to its right child. Following the unique directed path from the root to a terminal vertex will give a string of 0’s and 1’s. The set of all strings formed in this way will be a set of codewords with the prefix property, because corresponding to any codeword we can find the unique directed path by working down from the root of the binary tree, going left or right accordingly as each digit is 0 or 1. By definition we finish at a terminal vertex, and so this codeword cannot be the first part of another codeword.

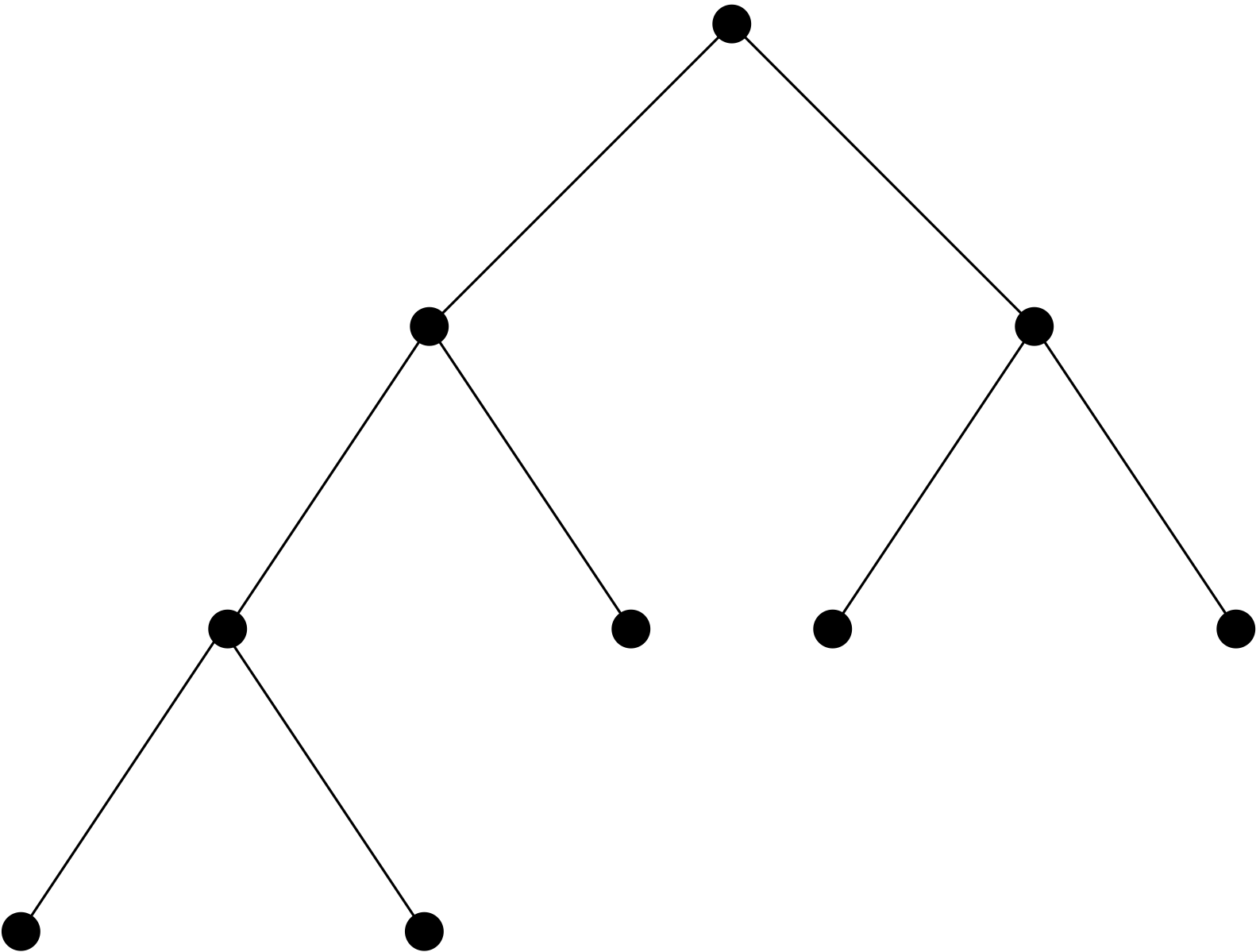
By using a binary tree we have found a way to produce codewords that have the prefix property. It remains to find a method for assigning shorter codewords to the more frequently used symbols.

Notice that these codewords correspond to the terminal vertices that are closest to the root. Thus, to obtain an efficient method for representing symbols by variable length codewords, we can use a binary tree and assign the most frequently used symbols to the terminal vertices that are closest to the root.

Suppose $w_{1}$ ,$w_{2}$ ,$\ldots$ ,$w_{k}$ are nonnegative real numbers. A binary tree for the weights $w_{1}$ ,$w_{2}$ ,$\ldots$ ,$w_{k}$ is a binary tree with $k$ terminal vertices labeled $w_{1},w_{2},\ldots,w_{k}$ . A binary tree for the weights $w_{1},w_{2},\ldots,w_{k}$ has total weight $d_{1}w_{1}+d_{2}w_{2}+\cdots +d_{k}w_{k}$ , where $d_{i}$ is the length of the directed path from the root to the vertex labeled $w_{i}$ $(i = 1, \ldots, k)$ .

For the coding problem we want to find a binary tree of smallest possible total weight in which the frequencies of the symbols to be encoded are the weights. A binary tree for the weights $w_{1}, w_{2},\ldots, w_{k}$ is called an optimal binary tree for the weights $w_{1}, w_{2}, \ldots, w_{k}$ when its total weight is as small as possible.

The following algorithm due to David A. Huffman produces an optimal binary tree for the weights $w_{1}, w_{2}, \ldots, w_{k}$ . The idea is to create a binary tree by using the two smallest weights, say $w_{1}$ and $w_{2}$ , replace $w_{1}$ and $w_{2}$ by $w_{1} + w_{2}$ in the list of weights, and then repeat the process.

For nonnegative real numbers $w_{1}, w_{2}, \ldots, w_{k}$ , this algorithm constructs an optimal binary tree for the weights $w_{1}, w_{2}, \ldots, w_{k}.$

Step 1 (select smallest weights). If there are two or more weights in the list of weights, select the two smallest weights, say $V$ and $W$ . (Ties can be broken arbitrarily.) Otherwise, we are done.

Step 2 (make binary tree). Construct a binary tree with the root assigned the label $V + W$ , its left child assigned the label $V$ , and its right child assigned the label $W$ . Include in this construction any binary trees that have the labels $V$ or $W$ assigned to a root. Replace $V$ and $W$ in the list of weights by $V + W$ . Go to step 1.

In order to find codewords with the prefix property such that the most frequently used symbols are assigned the shortest codewords, we construct an optimal binary tree with the stated frequencies of the symbols as its weights. Then by assigning 0’s and 1’s to the edges of this tree as described previously, codewords can be efficiently assigned to the various symbols.

Introduction to error-correcting codes

When a radio message is sent through space, interference with the transmission of a single letter or character may result in the receipt of an incorrect communication.

If the message NEXT STOP JOME is received, it may be clear that this was not the intended message. Perhaps the actual message was NEXT STOP ROME or NEXT STOP NOME, or something else.

It is often essential that a message be received as intended. For this reason, such messages are rarely sent in English (or French or German or any other common language), since transmission error often results in a misinterpretation.

To ensure the accuracy of a message, it is useful to encode it, that is, to use a new language in which it is less likely that two words will be confused with each other.

Definition 8.1 For an integer $b\geq 2$ , the set

of $b$ symbols is an_ alphabet. An ordered $n$ -tuple of symbols in $A$ is called a word of length $n$ _or simply an $n$ -word (over $A$ .)

Definition 8.2 For two $n$ -words $x$ and $y$ , the distance $d(x,y)$ , often called the Hamming distance, _between $x$ and $y$ is the number of coordinates at which $x$ and $y$ differ.

Example 8.9 _Let $x = 0101101$ , $y = 1011110$ and $z = 0111101$ . Then $d(x,y) = 5, d(x,z) = 1, d(y,z) = 4$ .

Theorem 8.1 The Hamming distance has the following properties.

1. $d(u,v)\geq 0$ , and $d(u,v)=0$ if and only if $u=v$ ;

2 $d(u,v)=d(v,u)$ for all $u,v\in V(G)$ ;

3 $d(u,v)\leq d(u,w)+d(w,v)$ for all $u,v,w\in V(G)$ (The triangle inequality)

Definition 8.3 Let $n$ be a positive integer and $A$ an alphabet of $b$ elements. A fixed-length code $C$ is a collection of words of length $n$ over $A$ . The fixed-length code $C$ is also called an $(n,b)$ -code. If $b=2$ , then $C$ is a binary code.

Definition 8.4 The distance $d(C)$ _of $C$ is

where the minimum is taken over all pairs $x,y$ of distinct code words.

The challenge in coding theory is to construct a code that

1. uses as simple an alphabet as possible to facilitate transmission of messages,

2. uses a sufficiently large $n$ so that many code words are available and so that there is a great enough distance between every two code words, and

3. uses a sufficiently small $n$ to simplify transmission of messages.

then what word was sent?

$t$ -error correcting codes

We now turn to the problem of constructing codes. Ideally, a code should be constructed so that even if a small number of errors do occur due to interference, the message can still be understood.

Definition 8.5 A code is $t$ -error correcting if, whenever a code word $x$ is transmitted, then $x$ is the unique code word closest to the word received, even when up to $t$ errors have occurred in the transmission of $x$ .

We assume that if there is a unique code word at minimum distance from the received word, then the received word was intended to be the code word.

What can we say about $d(C)$ ?

Theorem 8.2 A code $C$ is $t$ -error correcting if and only if $d(C)\geq 2t+1$ .

Proof: See lecture.

If an $(n,b)$ -code $C$ is $t$ -error correcting, there is a limit on how many code words $C$ can contain.

Theorem 8.3 If $C$ is a $t$ -error correcting $(n,b)$ -code, then

where

Definition 8.6 A $t$ -error correcting $(n,b)$ -code $C$ is perfect if $|C|=b^n/s$ , where $s$ is given by the above theorem. (That is, for every $n$ -word $w$ over the alphabet $\{0,1,\ldots,b-1\}$ , there is exactly one code word in $C$ within a distance of at most $t$ from $w$ .)

Consider the graph $G$ on $\{ 0,1, \dots, b-1 \}^n$ where there is an edge between vertices $u=(u_1,u_2,\ldots, u_n)$ and $v=(v_1, v_2, \ldots, v_n)$ if and only if $u_i\not = v_i$ for exactly one $i$ ($1\leq i \leq n$ ). A code can be considered as a subset of $G$ .

The Hamming distance between two code words is the same as the length of the shortest path in $G$ between the two corresponding vertices. For a good code (i.e., one with a large distance), the code words are placed at suitably selected vertices of $G$ so that the minimum distance among all pairs of code words is as large as possible.

RSA public-key cryptosystem

Consider the following problems:

1. PRIME: Is $n$ a prime number?

2. COMPOSITE: Is $n$ a composite number?

3. FACTORIZE: Find $a,b<n$ , if possible, such that $n=ab$ . Otherwise report that none exist (and that, for $n\geq 2$ , $n$ is prime.)

We have listed problems in this form in order to pinpoint the difference between COMPOSITE and FACTORIZE, which at first sight look as if they might be the same. Actually it is the first two, PRIME and COMPOSITE that are identical in their complexity.

Although FACTORIZE may look the same as COMPOSITE, it is in reality asking for a lot more, namely an explicit factorization. If we can find $a$ and $b$ less than $n$ such that $n=ab$ , then we automatically know that $n$ is composite, but the point is that there are circumstances under which we are able to assert that $n$ is composite without any factors being explicitly given.

A standard result in elementary number theory, known as ‘Fermat’s little theorem’, illustrates how this can happen.

Theorem 8.4 If $p$ is a prime number, then for any integer $a$ , $a^p\equiv a\mod p,$ and if p does not divide $a<$ then $a^{p-1}\equiv 1\mod p.$

Example 8.16 _Suppose that, for some $n$ and $a$ , we find that $a^n\not\equiv a\mod n$ . It immediately follows from Fermat’s little theorem that $n$ cannot be prime, so (if $n\geq 2$ ) it must be composite. But the method of showing this is rather indirect, and the computation that $a^{n-1}\not\equiv 1 \mod n$ may not itself tell us anything about the factorization of $n$ .

The theorem and example show that it is sometimes possible to discover that a number $n$ is composite without actually finding any of its factors. A more elaborate version of these ideas leads to the Miller-Rabin primality test which, assuming the Riemann hypothesis is true, determines whether an integer is prime or composite in polynomial time. A different method, which determines primality in polynomial time without any assumptions, is due to Agrawal, Kayal and Saxena.

The apparent difficulty of factorizing large numbers, and the comparative ease of producing large primes, has given rise to one of the most popular ‘public-key cryptosystems’, called the RSA system after its inventors Ronald Rivest, Adi Shamir and Leonard Adleman.

The idea of a public-key cryptosystem is that there is a public key and a private key. Everyone can know the public key, but the private key must be kept secret. Using the public key, anyone can encrypt a message to get a ciphertext. Determining the message in a given ciphertext should be extremely hard without the private key. The important mathematical notion is that of a ‘trapdoor’ or one-way function: namely a function which is easy to compute, but whose inverse is hard to compute without some additional information.

Most importantly, public key cryptography can be used for digital signatures, which solve the authentication problem. For example, how do you know that your automatic software updates are not a virus? The software update comes with a digital signature (generated by the software vendor) which can be verified using a public key “hard-wired” into the operating system/application. Enabling secure automatic updates would have been a real headache without public key cryptography.

Suppose that $p$ and $q$ are chosen as two distinct ‘large’ prime numbers, and let $n=pq$ . Once the encryption procedure has been carried out (that is, input has been stored in a coded, ‘secret’ form), the special knowledge needed for decryption (or recovering the input), called a private key, is a number $d$ between 1 and $n$ which is coprime with $(p-1)(q-1)$ , that is, $d$ and $(p-1)(q-1)$ share no common factor.

As $\gcd(d,(p-1)(q-1))=1$ , by Euclid’s algorithm there are integers $e$ and $b$ such that $ed+b(p-1)(q-1)=1$ . We assume that $0\leq e< (p-1)(q-1).$ The public key, the Information required for encryption is then the pair $(e,n)$ .

Now we describe how an integer $M$ in the range $0$ to $n-1$ (public key cryptography is mainly used to transmit symmetric session keys; so there is no loss of generality in assuming the message is a moderate-sized integer) is encrypted using the public key. We write the encrypted version as $f(M)$ , so that $f$ is the trapdoor function mentioned above. We let

Suppose that we are also in possession of the private key, $d$ . This may then be used to ‘decrypt’ the original value $M$ from its encrypted version $f(M)$ by using

To check the truth of this equation, since $0\leq M\leq n-1$ it is enough to show that $M^{ed}\equiv M\mod n$ . Now $p$ and $q$ are distinct primes and so this amounts to show that $M^{ed}\equiv M \mod p$ and $M^{ed}\equiv M \mod q.$

Now we describe how to make digital signature using RSA. A document or file is passed through a “hash function” to obtain an integer $M$ . A signature is generated (by the user who knows the private key) as

The receiver gets the document and $S$ , as well as the public key $(n,e)$ . They also use the hash function to compute $M$ and then verify the equation

For the method to be useful, two properties are required:

1. (Efficiency) It must be possible to carry out the arithmetic involved in selecting $p,q$ and $d$ , and in calculating the encrypted and decrypted numbers reasonably quickly (by computer), given the relevant keys.

2. (Security) It must be prohibitively costly to decrypt the encrypted version of the message without possession of the private key.

Selecting $p,q$ and $d$

First, one selects $p$ and $q$ of the desired size using the primality test mentioned above. Next, to select $d$ , it is sufficient to take a prime number larger than $p$ and $q$ (and below $pq$ ) since all prime factors of $(p-1)(q-1)$ must be less than any number so chosen.

To perform the encryption and decryption, we have to see how powers $\mod n$ can be rapidly computed.

In general, if $e$ has $k$ binary digits, $l$ of them 1s, in its binary expansion, then it will require $k+l-2$ multiplications $mod n$ to evaluate $M^e \mod n$ which is $O(\log n).$

A justification of property 2 is more a matter of faith at present, but certainly no easy method of decryption is known which does not essentially involve factorization of $n$ .

Given that the system stands or falls on the difficulty of factorizing large numbers, how large do $p$ and $q$ have to be to make it reasonably secure? At present there are algorithms known which will factorize numbers of over 200 digits using massive distributed computation, so allowing for possible improvements in this it seems safe for the moment to employ primes $p$ and $q$ of at least 1000 bits (i.e., 300 digits; so that $n$ will have about 600 digits).